题目内容
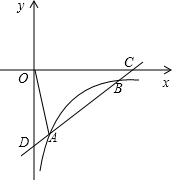 (2012•锦江区一模)如图,已知一次函数y=kx+b的图象交反比例函数y=
(2012•锦江区一模)如图,已知一次函数y=kx+b的图象交反比例函数y=| 4-2m |
| x |
| BC |
| AB |
| 1 |
| 3 |
(1)求m的值和一次函数的解析式;
(2)连接OA,求△OAC的面积.
分析:(1)过A作AE垂直于OC,交OC于点E,过B作BF⊥OC,交OC于点F,先把点A的坐标代入反比例函数表达式求出m的值,从而的反比例函数解析式,设点B的坐标为B(x,y),利用相似三角形对应边成比例求出y的值,然后代入反比例函数解析式求出点B的坐标,设出一次函数解析式为y=kx+b,将A和B的坐标代入得到关于k与b的方程组,求出方程组的解得到k与b的值,确定出一次函数解析式;
(2)由第一问求出的一次函数解析式,令y=0求出x的值,即为C的横坐标,确定出OC的长,由A的纵坐标确定出AE的长,以OC为底,AE为高,利用三角形的面积公式即可求出三角形AOC的面积.
(2)由第一问求出的一次函数解析式,令y=0求出x的值,即为C的横坐标,确定出OC的长,由A的纵坐标确定出AE的长,以OC为底,AE为高,利用三角形的面积公式即可求出三角形AOC的面积.
解答:解:(1)过A作AE⊥OC,交OC于点E,过B作BF⊥OC,交OC于点F,
∵点A(2,-4)在反比例函数图象上,
∴
=-4,
解得:m=6,
∴反比例函数解析式为y=-
,
∵∠AEC=∠BFC=90°,且∠BCF=∠ACE,
∴△BCF∽△ACE,
∴
=
,
∵
=
,∴
=
,
设点B的坐标为(x,y),
则点B到x轴的距离为-y,又点A到x轴的距离为4,
∴
=
=
,
解得y=-1,
∴-
=-1,
解得:x=8,
∴点B的坐标是B(8,-1),
设这个一次函数的解析式为y=kx+b,
∵点A、B是直线与反比例函数图象的交点,
∴
,
解得:
,
则一次函数解析式为y=
x-5;

(2)令y=
x-5中y=0,
解得:x=10,
则C(10,0),即OC=10,
又∵A(2,-4),
∴AE=4,
则S△AOC=
OC•AE=
×4×10=20.
∵点A(2,-4)在反比例函数图象上,
∴
| 4-2m |
| 2 |
解得:m=6,
∴反比例函数解析式为y=-
| 8 |
| x |
∵∠AEC=∠BFC=90°,且∠BCF=∠ACE,
∴△BCF∽△ACE,
∴
| BF |
| AE |
| BC |
| AC |
∵
| BC |
| AB |
| 1 |
| 3 |
| BC |
| AC |
| 1 |
| 4 |
设点B的坐标为(x,y),
则点B到x轴的距离为-y,又点A到x轴的距离为4,
∴
| -y |
| 4 |
| BC |
| AC |
| 1 |
| 4 |
解得y=-1,
∴-
| 8 |
| x |
解得:x=8,
∴点B的坐标是B(8,-1),
设这个一次函数的解析式为y=kx+b,
∵点A、B是直线与反比例函数图象的交点,
∴
|
解得:
|
则一次函数解析式为y=
| 1 |
| 2 |

(2)令y=
| 1 |
| 2 |
解得:x=10,
则C(10,0),即OC=10,
又∵A(2,-4),
∴AE=4,
则S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了反比例函数综合题,涉及的知识有:相似三角形的判定与性质,比例的性质,坐标与图形性质,待定系数法确定函数解析式,是一道较难的试题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
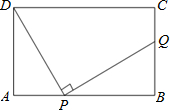 (2012•锦江区一模)如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由.
(2012•锦江区一模)如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由.