题目内容
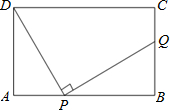 (2012•锦江区一模)如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由.
(2012•锦江区一模)如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由.分析:首先假设当m=10时,存在点P使得点Q与点C重合,易证得△PBC∽△DAP,然后由相似三角形的对应边成比例,即可求得此时AP的长.
解答: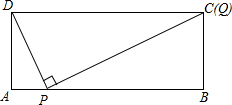 解:假设当m=10时,存在点P使得点Q与点C重合(如下图),
解:假设当m=10时,存在点P使得点Q与点C重合(如下图),
∵四边形ABCD是矩形,
∴∠B=∠A=90°,
∵PQ⊥PD,
∴∠DPC=90°,
∴∠APD+∠BPC=90°,
又∵∠ADP+∠APD=90°,
∴∠BPC=∠ADP,
∴△PBC∽△DAP,
∴
=
,
∴
=
,
∴AP=2或8,
∴存在点P使得点Q与点C重合,此时AP的长2或8.
 解:假设当m=10时,存在点P使得点Q与点C重合(如下图),
解:假设当m=10时,存在点P使得点Q与点C重合(如下图),∵四边形ABCD是矩形,
∴∠B=∠A=90°,
∵PQ⊥PD,
∴∠DPC=90°,
∴∠APD+∠BPC=90°,
又∵∠ADP+∠APD=90°,
∴∠BPC=∠ADP,
∴△PBC∽△DAP,
∴
| PB |
| DA |
| BC |
| AP |
∴
| 10-AP |
| 4 |
| 4 |
| AP |
∴AP=2或8,
∴存在点P使得点Q与点C重合,此时AP的长2或8.
点评:此题考查了相似三角形的判定与性质与矩形的性质.此题难度适中,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
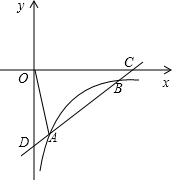 (2012•锦江区一模)如图,已知一次函数y=kx+b的图象交反比例函数y=
(2012•锦江区一模)如图,已知一次函数y=kx+b的图象交反比例函数y=