题目内容
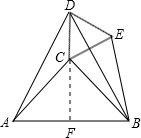
如图,△ABD和△CED均为等边三角形,AC=BC,AC⊥BC.若BE=
,则CD=______.

| 2 |

∵CA=CB,DA=DB
∴CD均在线段AB的垂直平分线上,即DF⊥AB,且∠CDB=30°
∴BD为等边△CDE中∠CDE的角平分线,∠CDB=∠EDB
在△CDB和△EDB中,
∴△CDB≌△EDB(SAS),
∴BE=BC.
∵AC=BC=
,
∴AB=
=2,且DF=
=
,
且CF=BF=1,
∴CD的长为DF-CF=
-1.
故答案为
-1.
∴CD均在线段AB的垂直平分线上,即DF⊥AB,且∠CDB=30°
∴BD为等边△CDE中∠CDE的角平分线,∠CDB=∠EDB
在△CDB和△EDB中,
|
∴△CDB≌△EDB(SAS),
∴BE=BC.
∵AC=BC=
| 2 |
∴AB=
| AC2+BC2 |
| BD2-BF2 |
| 3 |
且CF=BF=1,
∴CD的长为DF-CF=
| 3 |
故答案为
| 3 |


练习册系列答案
相关题目



