题目内容
【题目】某公司准备销售甲、乙两种材料中的一种,设年销售量为![]() (单位:吨)(
(单位:吨)(![]() ),若销售甲种材料,每吨成本为10万元,每吨售价
),若销售甲种材料,每吨成本为10万元,每吨售价![]() (单位:万元)与
(单位:万元)与![]() 的函数关系是:
的函数关系是:![]() ,设年利润为
,设年利润为![]() (单位:万元)(年利润=销售额-成本);若销售乙种材料,销售利润
(单位:万元)(年利润=销售额-成本);若销售乙种材料,销售利润![]() 与
与![]() 的函数关系是:
的函数关系是:![]() ,同时每吨可获返利
,同时每吨可获返利![]() 万元(
万元(![]() ),设年利润为
),设年利润为![]() (单位:万元)(年利润=销售利润+返利).
(单位:万元)(年利润=销售利润+返利).
(1)当![]() 时,
时,![]() ________;
________;
(2)当![]() ,
,![]() 时,
时,![]() ________;
________;
(3)求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 为何值时,
为何值时,![]() 最大,最大值是多少?
最大,最大值是多少?
【答案】(1)64;(2)60;(3)当![]() 时,
时,![]() 最大,最大值为84
最大,最大值为84
【解析】
解:(1)64;
【解法提示】当![]() 时,
时,![]() ;
;
(2)60;
【解法提示】当![]() 时,
时,
![]() ;
;
(3)由题意得![]() ,
,
∵![]() ,对称轴为
,对称轴为![]() ,
,
∴当![]() 时,
时,![]() 随x的增大而增大,
随x的增大而增大,
∴当![]() 时,
时,![]() 最大,最大值
最大,最大值![]() (万元).
(万元).

【题目】(2017陕西)养成良好的早锻炼习惯,对学生的学习和生活都非常有益.某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() (分钟)进行了调查.现把调查结果分成
(分钟)进行了调查.现把调查结果分成![]() 四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 | 时间 |
|
|
|
|
|
|
|
|
所抽取七年级学生早锻炼时间统计图
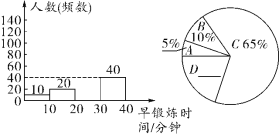
请你根据以上提供的信息,解答下列问题:
(1)补全频数分布直方图和扇形统计图;
(2)所抽取的七年级学生早锻炼时间的中位数落在________区间内;
(3)已知该校七年级共有1200名学生,请你估计这个年级学生中约有多少人一天早锻炼的时间不少于20分钟.(早锻炼:指学生在早晨7:00~7:40之间的锻炼)
【题目】某垃圾处理厂,只能处理![]() 、
、![]() 两类垃圾,且每天只能处理其中的一类垃圾,已知该垃圾厂每月工作25天,每天处理垃圾种类的吨数及费用如下表:
两类垃圾,且每天只能处理其中的一类垃圾,已知该垃圾厂每月工作25天,每天处理垃圾种类的吨数及费用如下表:
|
| |
每天处理的吨数(单位:吨) | 22 | 30 |
每吨处理的费用(单位:元) | 150 | 100 |
设该垃圾厂每月处理![]() 类垃圾
类垃圾![]() 天,这个厂每月处理垃圾的总吨数为
天,这个厂每月处理垃圾的总吨数为![]() 吨,每月处理垃圾所需的总费用为
吨,每月处理垃圾所需的总费用为![]() 元,据测算该厂每月最多处理垃圾590吨.
元,据测算该厂每月最多处理垃圾590吨.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)![]() 为何值时,
为何值时,![]() 最小,最小值是多少?
最小,最小值是多少?
(3)一段时间后,由于改进了处理![]() 类垃圾的流程,使处理每吨
类垃圾的流程,使处理每吨![]() 类垃圾的费用减少了
类垃圾的费用减少了![]() 元(
元(![]() ),
),![]() 类垃圾的处理费用没有改变,求该厂每月处理垃圾费用最少时,处理
类垃圾的处理费用没有改变,求该厂每月处理垃圾费用最少时,处理![]() 、
、![]() 两类垃圾的天数各是多少?
两类垃圾的天数各是多少?