题目内容
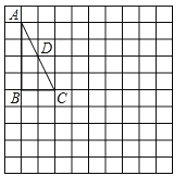
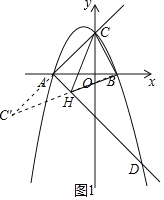
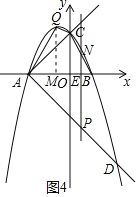
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣2,0)和B(l,0),与y轴交于点C.
(1)求抛物线的表达式;
(2)作射线AC,将射线AC绕点A顺时针旋转90°交抛物线于另一点D,在射线AD上是否存在一点H,使△CHB的周长最小.若存在,求出点H的坐标;若不存在,请说明理由;
(3)在(2)的条件下,点Q为抛物线的顶点,点P为射线AD上的一个动点,且点P的横坐标为t,过点P作x轴的垂线l,垂足为E,点P从点A出发沿AD方向运动,直线l随之运动,当﹣2<t<1时,直线l将四边形ABCQ分割成左右两部分,设在直线l左侧部分的面积为S,求S关于t的函数表达式.
【答案】(1)y=﹣x2﹣x+2;(2)点H坐标为(﹣![]() ,﹣
,﹣![]() );(3)
);(3)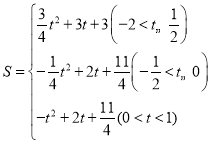 .
.
【解析】
(1)根据A,B坐标写出交点式,可得函数解析式;
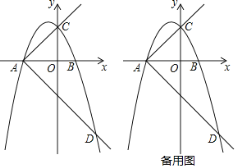
(2)如图1,延长CA到C',使AC'=AC,连接BC',BC'与AD的交点即为满足条件的点H,分别求出AC与AD的解析式和点C坐标,再求出BC'解析式,联立AD与BC'的解析式,可得点H;
(3)存在3种情况,一种是点P在抛物线对称轴的左侧,一种是在右侧且在x轴负半轴,还有一种是在x轴正半轴,然后再根据几何图形特点求解.
(1)抛物线与x轴交于点A(﹣2,0)和B(l,0)
∴交点式为y=﹣(x+2)(x﹣1)=﹣(x2+x﹣2)
∴抛物线的表示式为y=﹣x2﹣x+2
(2)在射线AD上存在一点H,使△CHB的周长最小.
如图1,延长CA到C',使AC'=AC,连接BC',BC'与AD交点即为满足条件的点H
∵x=0时,y=﹣x2﹣x+2=2
∴C(0,2)
∴OA=OC=2
∴∠CAO=45°,直线AC解析式为y=x+2
∵射线AC绕点A顺时针旋转90°得射线AD
∴∠CAD=90°
∴∠OAD=∠CAD﹣∠CAO=45°
∴直线AD解析式为y=﹣x﹣2
∵AC'=AC,
∴C'(﹣4,﹣2),
设直线BC'解析式为y=kx+a
∴![]()
解得: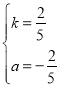
∴直线BC':y=![]() x﹣
x﹣![]()
∵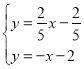 ,解得:
,解得: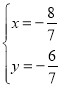 ,
,
∴点H坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)∵y=﹣x2﹣x+2=﹣(x+![]() )2+
)2+![]()
∴抛物线顶点Q(﹣![]() ,
,![]() )
)
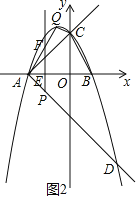
①当﹣2<t≤﹣![]() 时,如图2,直线l与线段AQ相交于点F
时,如图2,直线l与线段AQ相交于点F
设直线AQ解析式为y=mx+n
∴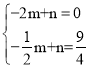 ,解得:
,解得: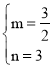
∴直线AQ:y=![]() x+3
x+3
∵点P横坐标为t,PF⊥x轴于点E
∴F(t,![]() t+3)
t+3)
∴AE=t﹣(﹣2)=t+2,FE=![]() t+3,
t+3,
∴S=S△AEF=![]() AEEF=
AEEF=![]() (t+2)(
(t+2)(![]() t+3)=
t+3)=![]() t2+3t+3;
t2+3t+3;
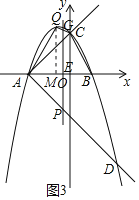
②当﹣![]() <t≤0时,如图3,直线l与线段QC相交于点G,过点Q作QM⊥x轴于M
<t≤0时,如图3,直线l与线段QC相交于点G,过点Q作QM⊥x轴于M
∴AM=﹣![]() ﹣(﹣2)=
﹣(﹣2)=![]() ,QM=
,QM=![]()
∴S△AQM=![]() AMQM=
AMQM=![]()
设直线CQ解析式为y=qx+2
把点Q代入:﹣![]() q+2=
q+2=![]() ,解得:q=﹣
,解得:q=﹣![]()
∴直线CQ:y=﹣![]() x+2
x+2
∴G(t,﹣![]() t+2)
t+2)
∴EM=t﹣(﹣![]() )=t+
)=t+![]() ,GE=﹣
,GE=﹣![]() t+2
t+2
∴S梯形MEGQ=![]() (QM+GE)ME=
(QM+GE)ME=![]() (
(![]() ﹣
﹣![]() t+2)(t+
t+2)(t+![]() )=﹣
)=﹣![]() t2+2t+
t2+2t+![]()
∴S=S△AQM+S梯形MEGQ=![]() +(﹣
+(﹣![]() t2+2t+
t2+2t+![]() )=﹣
)=﹣![]() t2+2t+
t2+2t+![]() ;
;
③当0<t<1时,如图4,直线l与线段BC相交于点N
设直线BC解析式为y=rx+2
把点B代入:r+2=0,解得:r=﹣2
∴直线BC:y=﹣2x+2
∴N(t,﹣2t+2)
∴BE=1﹣t,NE=﹣2t+2
∴S△BEN=![]() BENE=
BENE=![]() (1﹣t)(﹣2t+2)=t2﹣2t+1
(1﹣t)(﹣2t+2)=t2﹣2t+1
∵S梯形MOCQ=![]() (QM+CO)OM=
(QM+CO)OM=![]() ×(
×(![]() +2)×
+2)×![]() =
=![]() ,S△BOC=
,S△BOC=![]() BOCO=
BOCO=![]() ×1×2=1
×1×2=1
∴S=S△AQM+S梯形MOCQ+S△BOC﹣S△BEN=![]() +
+![]() +1﹣(t2﹣2t+1)=-t2+2t+
+1﹣(t2﹣2t+1)=-t2+2t+![]() ;
;
综上所述,S=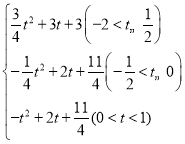

【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
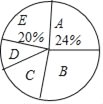
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?