题目内容
【题目】如图,AB为一斜坡,其坡角为19.5°,紧挨着斜坡AB底部A处有一高楼,一数学活动小组量得斜坡长AB=15m,在坡顶B处测得楼顶D处的仰角为45°,其中测量员小刚的身高BC=1.7米,求楼高AD.
(参考数据:sin19.5°≈ ![]() ,tan19.5°≈
,tan19.5°≈ ![]() ,最终结果精确到0.1m).
,最终结果精确到0.1m).
【答案】解:作CF⊥AD于点F.
在Rt△ABE中,∵AB=15,
∴BE=ABsin19.5°=15sin19.5°,
AE=ABcos19.5°=15cos19.5°,
在Rt△CDF中,∵CF=AE,∠DCF=45°,
∴DF=CF,
∴AD=DF+AF=CF+BC+BE=15cos19.5°+1.7+15sin19.5°≈21.0(m).
答:楼高AD为21.0米.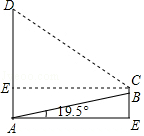
【解析】作CF⊥AD于点F,在直角△ABE中求得BE,和AE的长,然后在直角△CDE中利用三角函数求得DE的长,根据AD=DF+AF=CF+BC+BE求解.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.

练习册系列答案
相关题目