题目内容
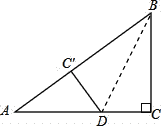
【题目】已知,如图,在三角形![]() 中,
中,![]() ,
,![]() 于
于![]() ,且
,且![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时点
;同时点![]() 由
由![]() 点出发,沿
点出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ,过点
,过点![]() 的动直线
的动直线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,设运动时间为
,设运动时间为![]()
![]() ,解答下列问题:
,解答下列问题:

(1)线段![]() _________
_________![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形?
为顶点的四边形为平行四边形?
【答案】(1)12;(2)证明见详解;(3)![]() 或t=4s.
或t=4s.
【解析】
(1)由勾股定理求出AD即可;
(2)由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB,再由等腰三角形的判定定理即可得出结论;
(3)分两种情况:①当点M在点D的上方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AD-AM=12-4t,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可;
②当点M在点D的下方时,根据题意得:PQ=BP=t,AM=4t,AD=12,得出MD=AM-AD=4t-12,由PQ∥MD,当PQ=MD时,四边形PQDM是平行四边形,得出方程,解方程即可.
(1)解:∵BD⊥AC,
∴∠ADB=90°,
∴![]() (cm),
(cm),
(2)如图所示:
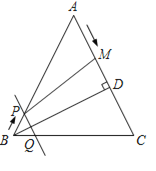
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
(3)分两种情况:
①当点M在点D的上方时,如图2所示:
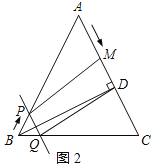
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AD-AM=12-4t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=12-4t,时,四边形PQDM是平行四边形,
解得:![]() (s);
(s);
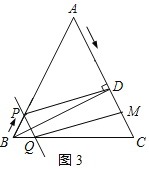
②当点M在点D的下方时,如图3所示:
根据题意得:PQ=BP=t,AM=4t,AD=12,
∴MD=AM-AD=4t-12,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=4t-12时,四边形PQDM是平行四边形,
解得:t=4(s);
综上所述,当![]() 或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形.
或t=4s时,以P、Q、D、M为顶点的四边形为平行四边形.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案