题目内容
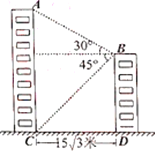
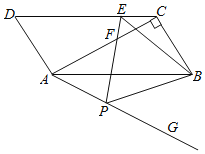
【题目】如图,在ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2![]() ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,则AF=_____.
【答案】![]()
【解析】
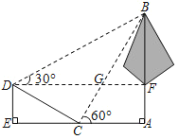
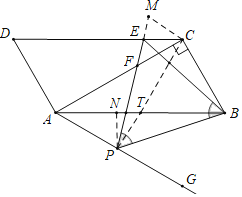
如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.首先证明∠APC=90°,解直角三角形求出AC,PA,利用相似三角形的性质求出CM,由CM∥PA,推出![]() ,由此即可解决问题.
,由此即可解决问题.
解:如图,连接PC交AB于T,作PN⊥AB于N,CM⊥PC交PE的延长线于M.
∵AC⊥BC,
∴∠ACB=90°,
∵BC=![]() ,∠BAC=30°,
,∠BAC=30°,
∴AB=2BC=![]() ,AC=
,AC=![]() BC=6,∠ABC=60°,
BC=6,∠ABC=60°,
∵∠EPB=∠EBP=60°,
∴△EPB是等边三角形,
∴∠PEB=60°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BCE=180°﹣∠ABC=120°,
∴∠EPB+∠BCE=180°,
∴P,B,C,E四点共圆,
∴∠PCB=∠PEB=60°,∠MPC=∠EBC,
∵∠TCB=∠CBT=60°
∴△TCB是等边三角形,
∴∠BCT=60°,∠ACT=30°,BT=BC=AT=![]() ,
,
∵∠BAG=∠BAC=30°,
∴∠APC=90°,
∴PA=ATcos30°=3,AN=PAcos30°=![]() ,PN=
,PN=![]() PA=
PA=![]() ,PC=
,PC=![]() PA=
PA=![]() ,
,
∴BN=AB﹣AN=![]() ,
,
∵∠PBE=∠CBT=60°,
∴∠PBN=∠CBE=∠CPM,
∵∠PCM=∠PNB=90°,
∴△PCM∽△BNP,
∴![]() ,
,
∴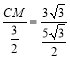 ,
,
∴CM=![]() ,
,
∵PA⊥PC,CM⊥PC,
∴CM∥PA,
∴ ,
,
∴AF=![]() AC=
AC=![]() .
.
故答案为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某电视机厂要印制产品宣传材料甲印刷厂提出:每份材料收1元印制费,另需收取所有印制材料的制版费1500元;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设该电视厂在同一个印刷厂一次印的数量为![]() 份
份![]() .
.
(1)根据题意填表:
一次印制数量(份) | 300 | 500 | 1500 | … |
甲印刷厂花费(元) | 2000 | … | ||
乙印刷厂花费(元) | 1250 | … |
(2)设在甲印刷厂花费![]() 元,在乙印刷厂花费
元,在乙印刷厂花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若电视厂在甲印刷厂和在乙印刷厂一次印制宣传材料的数量相同,且花费相同,则该电视厂在同一个印刷厂一次印制材料的数量为 份;
②印制800份宣传材料时,选择 印刷厂比较合算;
③电视机厂拟拿出3000元用于印制宣传材料,在 印刷厂印制宣传材料可以多一些.