题目内容
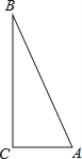
【题目】实践操作:如图,△ABC是直角三角形,∠ACB=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作∠BAC的平分线,交BC于点O;②以点O为圆心,OC为半径作圆.
综合运用:在你所作的图中,
(1)直线AB与⊙O的位置关系是 ;
(2)证明: ![]() ;
;
(3)若AC=5,BC=12,求⊙O的半径.
【答案】实践操作:作图见解析;
综合运用:(1)相切;(2)证明见解析;(3)⊙O的半径为![]() .
.
【解析】试题分析:(1)、根据角平分线的性质得出OC=OD,从而得出圆与直线的位置关系;(2)、根据相切的性质以及公共角得出△ABC和△OBD相似,从而得出答案;(3)、根据题意得出AD=AC=5,AB=13,则BD=8,设半径为x,则OB=12-x,根据Rt△BOD的勾股定理求出x的值,得出圆的半径.
试题解析:实践操作,如图所示:
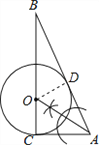
综合运用:
(1)相切
(2)因为∠BCA=90°,∠BDO=90°, 所以△ABC∽△OBD;
所以![]() 即
即![]() .
.
(3)因为AC=5,BC=12, 所以AD=5,AB=13, 所以DB=13﹣5=8,
设半径为x ,则OC=OD=x ,BO=(12﹣x), x2+82=(12﹣x)2,
解得:x=![]() .答:⊙O的半径为
.答:⊙O的半径为![]() .
.

练习册系列答案
相关题目