题目内容
【题目】如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
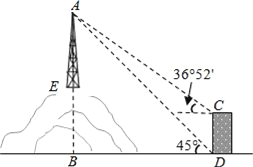
【答案】该铁塔的高AE为58米.
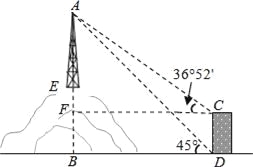
【解析】试题分析:根据楼高和山高可求出EF,继而得出AF,在Rt△AFC中表示出CF,在Rt△ABD中表示出BD,根据CF=BD可建立方程,解出即可.
试题解析:如图,过点C作CF⊥AB于点F.
设塔高AE=x,作CF⊥AB于点F,
则四边形BDCF是矩形,
∴CD=BF=30m,CF=BD,
∵在Rt△ADB中,∠ADB=45°,
∴AB=BD=x+62,
∵在Rt△ACF中,∠ACF=36°52′,CF=BD=x+62,AF=x+62﹣30=x+32,
∴tan36°52′=![]() ≈0.75,
≈0.75,
∴x=58.
答:该铁塔的高AE为58米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目