Question

【题目】如图，已知：AB∥CD，E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，试说明：
（1）AF∥ED；
（2）∠1=∠2．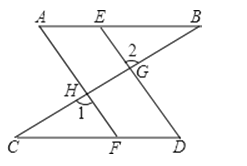

Answer 1

【答案】证明（1）：∵AB∥CD，
∴∠A=∠AFC，
∵∠A=∠D，
∴∠AFC=∠D，
∴AF∥ED；
（2）证明：∵AF∥ED，
∴∠1=∠CGD，
又∵∠2=∠CGD，
∴∠1=∠2．
【解析】（1）要证明AF∥ED，根据平行线的判定，只要找到可以判定AF∥ED的条件即可，由题意可以得到，同位角∠AFC=∠D，本题得以解决；
（2）根据第一问的结论AF∥ED，以及对顶角相等，可以证明结论成立．
【考点精析】根据题目的已知条件，利用平行线的判定与性质的相关知识可以得到问题的答案，需要掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．