题目内容
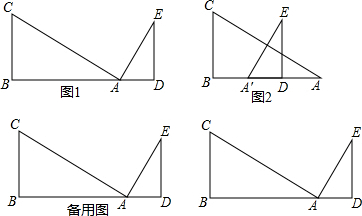
已知,Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,∠CAB=30°,∠DAE=60°,AD=3,AB=6| 3 |
(1)当顶点E恰好移动到边AC上时,求此时对应的x值;
(2)在平移过程中,设△A′DE与Rt△ABC重叠部分的面积为S,请直接写出S与x之间的函数关系式以及相应的自变量x的取值范围;
(3)过点C作CF∥AE交AB的延长线于点F,点M为直线BC上一动点,连接FM,得到△MCF,将△MCF绕点C逆时针旋转60°,得到△M′CF′(M的对应点为M′,F的对应点为F′),问△FMM′的面积能否等于
| 3 |
分析:(1)和(2)根据直角三角形的性质和三角形面积的求解方法,求出重叠面积S与x的函数关系式;
(3)根据题意,利用三角形的面积求解方法分三种情况讨论,列方程式解方程可求解出AM′的长度.
(3)根据题意,利用三角形的面积求解方法分三种情况讨论,列方程式解方程可求解出AM′的长度.
解答:解:(1)∵顶点E恰好移动到边AC上时,
∴x=3
×
+3=12
(2)当0≤x≤3时,S=
x2;
当3<x≤6
时,S=-
x2+
x-
;
当6
<x≤12时,S=-
x2+(18+
)x-
;
当12<x≤6
+3时,S=-
x2+18x-
.
(3)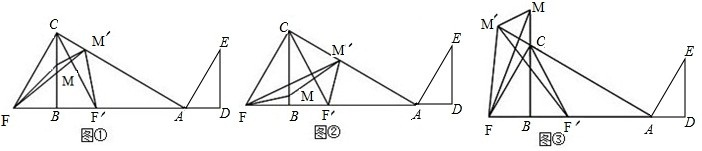
如图①所示:设CM=CM′=x,A E D
则S△FMM′=S△FCM′-S△FCM-S△MCM′
=
x•4
-
x•2
-
x2=
将其化简得:x2-4x+4=0
∴x=2
∴AM′=12-2=10
如图②所示:设CM=CM′=x,
则S△FMM′=S△FCM+S△MCM′-S△FCM′
=
x•2
+
x2-
x•4
=
将其化简得:x2-4x-4=0
∴x=2±2
(舍负)
∴x=2+2
∴AM′=12-(2+2
)=10-2
如图③所示:设CM=CM′=x,
S△FMM′=S△MCM′+S△FCM′-S△FCM
=
x2+
x•4
-
x•2
=
将其化简得:x2+4x-4=0
∴x=-2±2
(舍负)
∴x=-2+2
∴AM′=12+(-2+2
)=10+2
∴AM′的值为10或10-2
或 10+2
.
∴x=3
| 3 |
| 3 |
(2)当0≤x≤3时,S=
| ||
| 8 |
当3<x≤6
| 3 |
| ||
| 24 |
| 3 |
| 3 |
| 2 |
| 3 |
当6
| 3 |
13
| ||
| 24 |
| 3 |
111
| ||
| 2 |
当12<x≤6
| 3 |
| ||
| 2 |
99
| ||
| 2 |
(3)

如图①所示:设CM=CM′=x,A E D
则S△FMM′=S△FCM′-S△FCM-S△MCM′
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| 3 |
将其化简得:x2-4x+4=0
∴x=2
∴AM′=12-2=10
如图②所示:设CM=CM′=x,
则S△FMM′=S△FCM+S△MCM′-S△FCM′
=
| 1 |
| 2 |
| 3 |
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 3 |
将其化简得:x2-4x-4=0
∴x=2±2
| 2 |
∴x=2+2
| 2 |
∴AM′=12-(2+2
| 2 |
| 2 |
如图③所示:设CM=CM′=x,
S△FMM′=S△MCM′+S△FCM′-S△FCM
=
| ||
| 4 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
将其化简得:x2+4x-4=0
∴x=-2±2
| 2 |
∴x=-2+2
| 2 |
∴AM′=12+(-2+2
| 2 |
| 2 |
∴AM′的值为10或10-2
| 2 |
| 2 |
点评:此题主要考查了直角三角形判定与性质三角形面积求法等知识,利用平移性质得出对应边之间的关系是解题关键.

练习册系列答案
相关题目

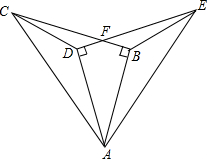 如图,已知在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,AC=AE,AD=AB,BC与DE相交于点F,连接CD,EB.
如图,已知在Rt△ABC和Rt△ADE中,∠ABC=∠ADE=90°,AC=AE,AD=AB,BC与DE相交于点F,连接CD,EB.