题目内容
已知等腰Rt△ABC和等腰Rt△EDF,其中D、G分别为斜边AB、EF的中点,连CE,又M为BC中点,N为CE的中点,连MN、MG
(1)如图1,当DE恰好过M点时,求证:∠NMG=45°,且MG=
MN;
(2)如图2,当等腰Rt△EDF绕D点旋转一定的度数时,第(1)问中的结论是否仍成立,并证明;
(3)如图3,连BF,已知P为BF的中点,连CF与PN,若CF=6,直接写出
=
.

(1)如图1,当DE恰好过M点时,求证:∠NMG=45°,且MG=
| 2 |
(2)如图2,当等腰Rt△EDF绕D点旋转一定的度数时,第(1)问中的结论是否仍成立,并证明;
(3)如图3,连BF,已知P为BF的中点,连CF与PN,若CF=6,直接写出
| PN |
| CF |
| ||
| 2 |
| ||
| 2 |

分析:(1)连接NG、CF,由题意可得CE=CF,易证MCGE四点共圆,即MN=NG,根据圆周角和圆心角的关系,可得∠MNG=90,即可证得;
(2)连接CF,CD,BE,NG,易证△BDE≌△CDF,则BE=CF,根据三角形中位线的性质,可得MN=NG,∠GNC+∠MNC=90°,即△MNG是等腰直角三角形,即可证得;
(3)连接PD,DM,PD为三角形ABF中位线,PD平行AF,PD=
AF,在三角形ABC中,DM为中位线,DM=
AC,MN=
BE=
CF,D,M,N共线,DN=
(BC+CF),BC=AC,DP=DN,三角形DPN是等腰直角三角形,PN/CF=
=
=
(
+1).
(2)连接CF,CD,BE,NG,易证△BDE≌△CDF,则BE=CF,根据三角形中位线的性质,可得MN=NG,∠GNC+∠MNC=90°,即△MNG是等腰直角三角形,即可证得;
(3)连接PD,DM,PD为三角形ABF中位线,PD平行AF,PD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| PB |
| CF |
| ||
| 2 |
| (AC+CF) |
| CF |
| ||
| 2 |
| AC |
| CF |
解答: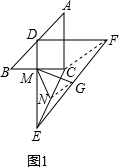 解:(1)连接CF、NG,如图,
解:(1)连接CF、NG,如图,
∴D、C、G三点共线,
∴CE=CF,DE⊥BC,
∵MN是直角三角形CME斜边上的中线,
∴MN=
CE,
又∵NG是三角形CEF的中位线,
∴NG=
CF,
∴NG=NM;
∴MCGE四点共圆,又∠MEG=45°,
∴∠MNG=90,即三角形MNG为等腰直角三角形,
∴∠NMG=∠NGM=45,MG=
MN.
(2)连接CF,CD,BE,NG,如图,
∵△ABC是等腰直角三角形,CD是底边中线,
∴CD⊥AB,∠ADC=90°,又∠EDF=90°,∠BDE=∠CDF,
在△BDE和△CDF中,
,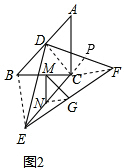
∴△BDE≌△CDF(SAS),
∴BE=CF,∠BED=∠DFC,
∵在△CBE中,MN是中线,
∴∠MNC=∠BEC,MN=
BE,
延长EC交DF于P,
∵在△ECF中,GN是中线,
∴GN=
CF,∠CNG=∠PCF,
∴∠MNC+∠CNG=∠BEC+∠PCF,
=(∠BED+∠DEP)+(∠DPE-∠PFC),
=∠DFC+∠DEP+∠DPE-∠DFC,
=∠DEP+∠DPE,
∵Rt△EDF中,∠EDF=90°,
∴∠DEP+∠DPE=180°-90°=90°,
∴∠MNG=90°,
∴△MNG是直角三角形,
又∵BE=CF,
∴MN=NG,
∴△MNG是等腰直角三角形,
∴∠NMG=∠NGM=45°,MG=
MN;
(3)
.
 解:(1)连接CF、NG,如图,
解:(1)连接CF、NG,如图,∴D、C、G三点共线,
∴CE=CF,DE⊥BC,
∵MN是直角三角形CME斜边上的中线,
∴MN=
| 1 |
| 2 |
又∵NG是三角形CEF的中位线,
∴NG=
| 1 |
| 2 |
∴NG=NM;
∴MCGE四点共圆,又∠MEG=45°,
∴∠MNG=90,即三角形MNG为等腰直角三角形,
∴∠NMG=∠NGM=45,MG=
| 2 |
(2)连接CF,CD,BE,NG,如图,
∵△ABC是等腰直角三角形,CD是底边中线,
∴CD⊥AB,∠ADC=90°,又∠EDF=90°,∠BDE=∠CDF,
在△BDE和△CDF中,
|

∴△BDE≌△CDF(SAS),
∴BE=CF,∠BED=∠DFC,
∵在△CBE中,MN是中线,
∴∠MNC=∠BEC,MN=
| 1 |
| 2 |
延长EC交DF于P,
∵在△ECF中,GN是中线,
∴GN=
| 1 |
| 2 |
∴∠MNC+∠CNG=∠BEC+∠PCF,
=(∠BED+∠DEP)+(∠DPE-∠PFC),
=∠DFC+∠DEP+∠DPE-∠DFC,
=∠DEP+∠DPE,
∵Rt△EDF中,∠EDF=90°,
∴∠DEP+∠DPE=180°-90°=90°,
∴∠MNG=90°,
∴△MNG是直角三角形,
又∵BE=CF,
∴MN=NG,
∴△MNG是等腰直角三角形,
∴∠NMG=∠NGM=45°,MG=
| 2 |
(3)
| ||
| 2 |
点评:本题主要考查了等腰直角三角形、旋转的性质、相似三角形的判定和性质,要熟练掌握等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质,要注意根据等腰三角形的性质和相似三角形的判定和性质,借助辅助线来解答.

练习册系列答案
相关题目

 (2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( )
(2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( ) (2012•拱墅区二模)如图,已知等腰Rt△ABC中,∠ACB=90°,点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
(2012•拱墅区二模)如图,已知等腰Rt△ABC中,∠ACB=90°,点D为等腰Rt△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA. 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,