Question

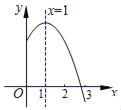
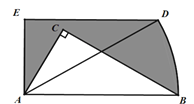
【题目】如图，在Rt△ABC中，∠ACB=90°，∠CAB=60°,AC=1，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE， 点B经过的路径为弧BD，则图中阴影部分的面积为_____________.

Answer 1

【答案】

【解析】

先根据含30°的直角三角形性质得到AB=2, 再根据扇形的面积公式计算出S扇形ABD，由旋转的性质得到Rt△ADE≌Rt△ACB，于是S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD．

解：∵∠ACB=90°，∠CAB=60°,AC=1，
∴∠CBA=30°，AB=2AC=2

∴S扇形ABD=

又∵Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，
∴Rt△ADE≌Rt△ACB，
∴S阴影部分=S△ADE+S扇形ABD-S△ABC=S扇形ABD=

故答案为：