题目内容
【题目】已知：正方形ABCD，E为平面内任意一点，连接DE，将线段DE绕点D顺时针旋转90°得到DG，连接EC，AG．
（1）当点E在正方形ABCD内部时， ①根依题意，在图1中补全图形；
②判断AG与CE的数量关系与位置关系并写出证明思路．
（2）当点B，D，G在一条直线时，若AD=4，DG=2 
，求CE的长．（可在备用图中画图） 
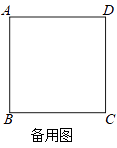
【答案】
（1）解：当点E在正方形ABCD内部时，
①根依题意，补全图形如图1：
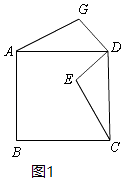
②AG=CE，AG⊥CE．
理由：
在正方形ABCD，
∴AD=CD，∠ADC=90°，
∵由DE绕着点D顺时针旋转90°得DG，
∴∠GDE=∠ADC=90°，GD=DE，
∴∠GDA=∠EDC
在△AGD和△CED中，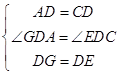 
，
∴△AGD≌△CED，
∴AG=CE．
延长CE分别交AG、AD于点F、H，
由①中结论△AGD≌△CED，
∴∠GAD=∠ECD，
∵∠AHF=∠CHD，
∴∠AFH=∠HDC=90°，
∴AG⊥CE．
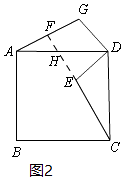
（2）解：①当点G在线段BD的延长线上时，如图3所示．
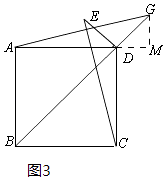
过G作GM⊥AD于M．
∵BD是正方形ABCD的对角线，
∴∠ADB=∠GDM=45°．
∵GM⊥AD，DG=2 
∴MD=MG=2，
∴AM=AD+DM=6
在Rt△AMG中，由勾股定理，得
AG= 
=2 
，
∴CE=AG=2
②当点G在线段BD上时，如图4所示，
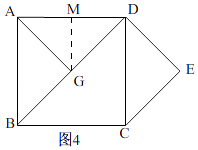
过G作GM⊥AD于M．
∵BD是正方形ABCD的对角线，
∴∠ADG=45°
∵GM⊥AD，DG=2
∴MD=MG=2，
∴AM=AD﹣MG=2
在Rt△AMG中，由勾股定理，得
AG= =2
∴CE=AG=2
故CE的长为2 或2 ．
【解析】（1）①根据题意补全图形，
②先判断出∠GDA=∠EDC，进而得出△AGD≌△CED，即可得出AG=CE，最后判断出∠AFH=∠HDC=90°即可得出结论；（2）分两种情况，①当点G在线段BD的延长线上时和②当点G在线段BD上时，构造直角三角形利用勾股定理即可得出结论．
【考点精析】解答此题的关键在于理解图形的旋转的相关知识，掌握每一个点都绕旋转中心沿相同方向转动了相同的角度，任意一对对应点与旋转中心的连线所成的角都是旋转角，对应点到旋转中心的距离相等．旋转的方向、角度、旋转中心是它的三要素．
