Question

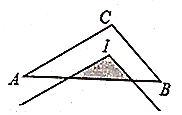
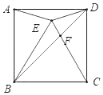
【题目】如图，正方形ABCD中，以BC为边向正方形内部作等边△BCE．连接AE．DE，连接BD交CE于F，下列结论：①∠AED＝150°②△DEF～△BAE；③tan∠ECD＝④△BEC的面积：△BFC的面积（+1）：2，其中正确的结论有（　　）个．

A.4B.3C.2D.1

Answer 1

【答案】A

【解析】

①利用正方形的性质，等边三角形的性质，等腰三角形的性质及三角形的内角和，周角求得判定即可；
②由①可得到∠ADE的度数，再利用正方形的性质即可得∠DEF=∠ABE，即可判定；
③可利用含30°的直角三角形的性质即可分别求出，再与tan∠ECD=tan30°作比较即可；
④两个三角形的底相同，由高的比进行判定即可.

∵△BEC为等边三角形

∴∠EBC＝∠BCE＝∠ECB＝60°，AB＝EB＝EC＝BC＝DC

∵四边形ABCD为正方形

∴∠ABE＝∠ECD＝90°﹣60°＝30°

∴在△ABE和△DCE中，

AB＝DC

∠ABE＝∠ECD

BE＝EC

∴△ABE≌△DCE（SAS）

∴∠AEB＝∠DEC＝＝75°

∴∠AED＝360°﹣60°﹣75°×2＝150°

故①正确

由①知AE＝ED

∴∠EAD＝∠EDA＝15°

∴∠EDF＝45°﹣15°＝30°

∴∠EDF＝∠ABE

由①知∠AEB＝∠DEC，

∴△DEF～△BAE

故②正确

过点F作FM⊥DC交于M，如图

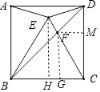
设DM＝x，则FM＝x，DF＝x

∵∠FCD＝30°

∴MC＝x

则在Rt△DBC中，BD＝

∴BF＝BD﹣DF＝

则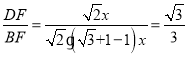

∵tan∠ECD＝tan30°＝

∴tan∠ECD＝

故③正确

如图过点E作EH⊥BC交于H，过F作FG⊥BC交于G，得

由③知MC＝，MC＝FG

∴FG＝

∵BC＝DC＝x

∴BH＝

∵∠EBC＝60°

∴EH＝

∴

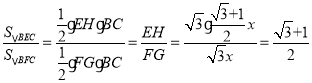
故④正确

故选：A．