题目内容
已知如图,在平行四边形 中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连结AN、CM。
中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连结AN、CM。
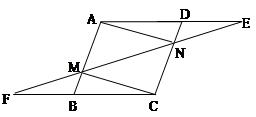
(1)求证:△DEN≌△BFM
(2)试判断四边形ANCM的形状,并说明理由。
 中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连结AN、CM。
中,延长AD到E,延长CB到F,使得DE=BF,连接EF,分别交AB、CD于点M、N,连结AN、CM。
(1)求证:△DEN≌△BFM
(2)试判断四边形ANCM的形状,并说明理由。
(1)证明 ,
, ,DE=BF得△DEN≌△BFM (2)四边形ANCM是平行四边形
,DE=BF得△DEN≌△BFM (2)四边形ANCM是平行四边形
 ,
, ,DE=BF得△DEN≌△BFM (2)四边形ANCM是平行四边形
,DE=BF得△DEN≌△BFM (2)四边形ANCM是平行四边形试题分析:(1)在平行四边形
 中,延长AD到E,延长CB到F,
中,延长AD到E,延长CB到F, ,AE//CF,
,AE//CF, ,
, ,
, ,又因为DE=BF,所以△DEN≌△BFM(ASA)
,又因为DE=BF,所以△DEN≌△BFM(ASA)(2)由(1)知△DEN≌△BFM,则DN=BM;在平行四边形
 中,AB//CD,AB=CD,∵AB//CD,所以AM//CN,又∵AB=CD,DN=BM,∴AM=AB-BM=CD-DN=CN,所以四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形)
中,AB//CD,AB=CD,∵AB//CD,所以AM//CN,又∵AB=CD,DN=BM,∴AM=AB-BM=CD-DN=CN,所以四边形ANCM是平行四边形(一组对边平行且相等的四边形是平行四边形)点评:本题考查三角形全等、平行四边形,要求考生掌握三角形全等是判定方法,熟悉平行四边形的性质,会判定四边形是平行四边形

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 中,
中, ,
, 为垂足.若
为垂足.若 ,则
,则 ( )
( )




 ,连接DE并延长交AB于M,连接BF交CD于N,
,连接DE并延长交AB于M,连接BF交CD于N,
 的值.
的值. ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③ ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。

 cm B.
cm B. cm
cm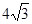 cm D.3 cm
cm D.3 cm
 中,
中, ,
, ,
, ,
, ,
, 为
为 上一动点,则
上一动点,则 周长的最小值为 .
周长的最小值为 .