Question

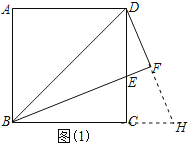
【题目】如图，在正方形ABCD中，E是CD边上一动点，DF⊥BE交BE的延长线于F．

（1）如图（1），若BE平分∠DBC时，

①直接写出∠FDC的度数；

②延长DF交BC的延长线于点H，补全图形，探究BE与DF的数量关系，并证明你的结论；

（2）如图（2），过点C作CG⊥BE于点G，猜想线段BF，CG，DF之间的数量关系，并证明你的猜想.

Answer 1

【答案】（1）①22.5°；②BE＝2DF，（2）BF＝2CG+DF

【解析】

（1）①根据正方形的性质得到∠DBC＝45°，根据角平分线的性质、三角形内角和定理计算，得到答案；

②根据题意补全图形，证明△BFD≌△BFH，得到DF＝FH＝DH，证明△BCE≌△DCH，根据全等三角形的性质证明结论；

（2）在BF上取点H，使FH＝DF，连接DH、FC，证明△BDH∽△CDF，得到，∠DBH＝∠DCF，根据等腰直角三角形的性质计算即可．

解：（1）①∵四边形ABCD为正方形，

∴∠DBC＝45°，

∵BE平分∠DBC，

∴∠DBE＝∠CBE＝22.5°，

∵∠F＝∠C＝90°，∠DEF＝∠BEC，

∴∠FDC＝∠CBE＝22.5°；

②补全图形如图（1）所示，

BE＝2DF，

理由如下：在△BFD和△BFH中，

，

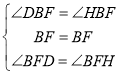∴△BFD≌△BFH（ASA）

∴DF＝FH＝DH，

在△BCE和△DCH中，

，

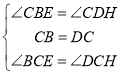∴△BCE≌△DCH（ASA）

∴BE＝DH＝2DF；

（2）BF＝2CG+DF

理由如下：在BF上取点H，使FH＝DF，连接DH、FC，

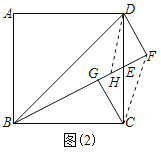
∵FD＝FH，∠DFH＝90°，

∴∠FHD＝∠FDH＝45°，DH＝DF，

∵∠BDC＝45°，

∴∠BDC＝∠HDF，

∴∠BDH＝∠CDF，

∵，∠BDH＝∠CDF，

∴△BDH∽△CDF，

∴，∠DBH＝∠DCF，

∵∠GBC＝90°﹣∠BCG＝∠GCH，

∴∠GCF＝∠DBC＝45°，

∴FC＝CG，

∴BH＝2CG，

∴BF＝BH+HF＝2CG+DF．