Question

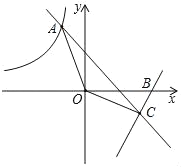
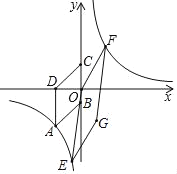
【题目】如图，在平面直角坐标系中，四边形ABCD为菱形，且点D(﹣4，0)在x轴上，点B和点C(0，3)在y轴上，反比例函数y＝(k≠0)过点A，点E(﹣2，m)、点F分别是反比例函数图象上的点，其中点F在第一象限，连结OE、OF，以线段OE、OF为邻边作平行四边形OEGF．

(1)写出反比例函数的解析式；

(2)当点A、O、F在同一直线上时，求出点G的坐标；

(3)四边形OEGF周长是否有最小值？若存在，求出这个最值，并确定此时点F的坐标，若不存在，请说明理由．

Answer 1

【答案】(1)；(2)点G的坐标为(2，﹣5)；(3)点F的坐标为(2，2)时，四边形OEGF周长最小，最小值为：4+4．

【解析】

（1）首先根据D点坐标，写出A点的横坐标，再计算CD的长，根据菱形的性质，可得A点的坐标，代入反比例函数，即可求得k的值，进而求得反比例函数的解析式.

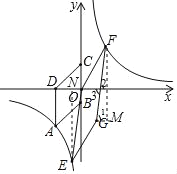
（2）首先将E点代入反比例函数，计算m,根据反比例函数的对称性，可得F点的坐标，再证明△ENO≌△FMG，故求得G点坐标.

（3）设出F点的坐标，利用勾股定理列方程，利用二次函数求解.

解：(1)∵点D(﹣4，0)在x轴上，

∴A点横坐标为：﹣4，

∵点C(0，3)在y轴上，

∴DC＝5，

∵四边形ABCD为菱形，

∴AD＝5，

∴点A的坐标为(﹣4，﹣5)，

则解析式为：；

(2)如图，∵x＝﹣2时，y＝＝﹣10，

∴点E的坐标为(﹣2，﹣10)，

∵点A、O、F在同一直线上，

∴A，F关于原点对称，

∴点F的坐标(4，5)，

分别过点E、F作EN⊥x轴于点N，FM⊥GM于点M，FM也垂直于x轴，

∵四边形OEGF是平行四边形，

∴EO∥FG，

∴∠NOE＝∠3，

∵∠2＝∠3＝∠1，

∴∠1＝∠NOE，

在△ENO和△FMG中

，

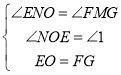∴△ENO≌△FMG(AAS)，

设点G的坐标为(m，n)，则5﹣n＝10，m﹣4＝﹣2，

故n＝﹣5，m＝2，

则点G的坐标为(2，﹣5)；

(3)由于OE为定值，则只需求出OF的最小值即可，

设点F的坐标为(a，)，

根据勾股定理得， ，

显然当a=时，OF2最小，即a＝2时，OF最小，OF＝2，

EO＝2，

因此，当点F的坐标为(2，2)时，四边形OEGF周长最小，

最小值为：4+4．