题目内容
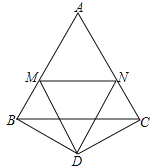
【题目】如图,![]() 是边长为1的等边三角形,
是边长为1的等边三角形,![]() 为顶角
为顶角![]() 的等腰三角形,点
的等腰三角形,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,则
,则![]() 的周长为( )
的周长为( )
A.2B.3C.1.5D.2.5
【答案】A
【解析】
延长AC到E,使CE=BM,连接DE,求证△BMD≌△CED,可得∠BDM=∠CDE,进而求证△MDN≌△EDN可得MN=NE=NC+CE=NC+BM,即可计算△AMN周长.
如图所示,延长AC到E,使CE=BM,连接DE,
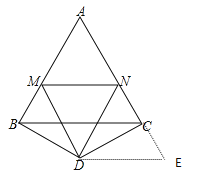
∵BD=DC,∠BDC=120°,
∴∠CBD=∠BCD=30°,
∵∠ABC=∠ACB=60°,
∴∠ABD=∠ACD=∠DCE=90°,
在△BMD和△CED中,
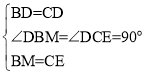
∴△BMD≌△CED(SAS),
∴∠BDM=∠CDE,DM=DE,
又∵∠MDN=60°,
∴∠BDM+∠NDC=60°,
∴∠EDC+∠NDC=∠NDE=60°=∠NDM,
在△MDN和△EDN中,
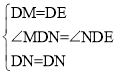
∴△MDN≌△EDN(SAS),
∴MN=NE=NC+CE=NC+BM,
所以△AMN周长=AM+AN+MN=AM+AN+NC+BM=AB+AC=2.
故选A.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目