题目内容
如图P为反比例函数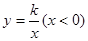 的图像上一点,过P向x轴轴作垂线所围成的矩形周长最小值为6,则k=
的图像上一点,过P向x轴轴作垂线所围成的矩形周长最小值为6,则k=

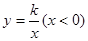 的图像上一点,过P向x轴轴作垂线所围成的矩形周长最小值为6,则k=
的图像上一点,过P向x轴轴作垂线所围成的矩形周长最小值为6,则k= 
- 

过P作PM垂直于x轴,PN垂直于y轴,根据题意得出矩形PMON是正方形时周长最小,由周长最小值为6求出此时正方形的边长为1.5,可得出PM=PN=1.5,再由P为第二象限的点,确定出P的坐标,将P的坐标代入反比例函数解析式中求出k的值即可.
过P作PM⊥x轴,PN⊥y轴,如图所示,
当矩形PMON为正方形时,周长最小为6,此时正方形的边长为1.5,
则PM=PN=1.5,
又∵P为第二象限的点,
∴P(-1.5,1.5),
将P的坐标代入反比例解析式得:1.5=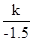 ,解得:k=-2.25.
,解得:k=-2.25.
故答案为:-2.25。
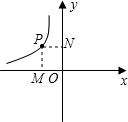
过P作PM⊥x轴,PN⊥y轴,如图所示,
当矩形PMON为正方形时,周长最小为6,此时正方形的边长为1.5,
则PM=PN=1.5,
又∵P为第二象限的点,
∴P(-1.5,1.5),
将P的坐标代入反比例解析式得:1.5=
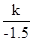 ,解得:k=-2.25.
,解得:k=-2.25. 故答案为:-2.25。


练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
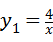 ,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是 
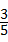 ,反比例函数
,反比例函数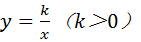 的图象经过AO的中点C,且与AB交于点D,则点D的坐标为____________.
的图象经过AO的中点C,且与AB交于点D,则点D的坐标为____________.
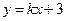 的图象与反比例函数
的图象与反比例函数 (
(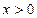 )的图象交于点
)的图象交于点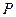 .
.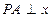 轴于点
轴于点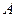 ,
,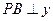 轴于点
轴于点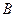 .一次函数的图象分别交
.一次函数的图象分别交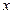 轴、
轴、 轴于点
轴于点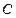 、点
、点 ,且
,且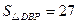 ,
,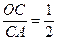 .
.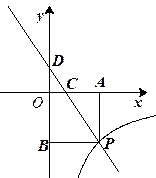
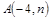 ,
,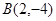 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数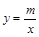 的图象的两个交点.
的图象的两个交点.
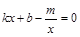 的解(请直接写出答案);
的解(请直接写出答案);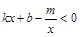 ,求x的取值范围.
,求x的取值范围.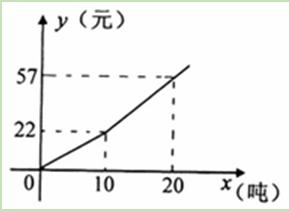
 图象上的是
图象上的是 的图象,当
的图象,当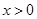 时,随的增大而增大,则的取值范围是
时,随的增大而增大,则的取值范围是
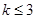
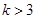

 的图象的任一支上,
的图象的任一支上,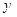 都随
都随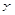 的增大而增大,则
的增大而增大,则 的值可以是
的值可以是