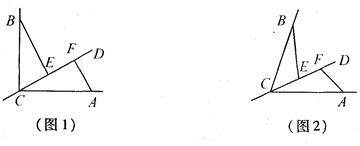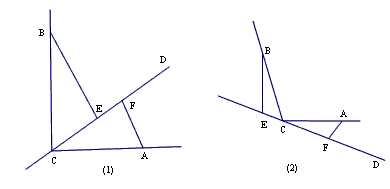��Ŀ����
CD�Ǿ�����BCA����C��һ��ֱ�ߣ�CA=CB��E��F�ֱ���ֱ��CD�����㣬�ҡ�BEC=��CFA=�Ϧ���

����ֱ��CD������BCA���ڲ�����E��F������CD�ϣ����������������⣺
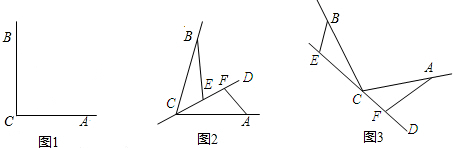
����ͼ1������BCA=90�㣬�Ϧ�=90�㣬��BE_____CF�� EF_____|BE-AF|���>������<����=������
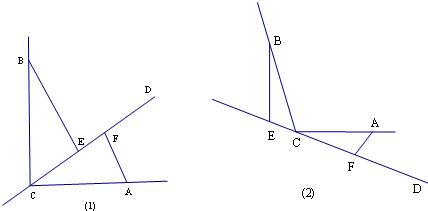
����ͼ2����0�㣼��BCA��180�㣬������һ�����ڡϦ����BCA��ϵ������_____��ʹ���е�����������Ȼ��������֤���������۳�����
����ͼ3����ֱ��CD������BCA���ⲿ���Ϧ�=��BCA�������EF��BE��AF�����߶�������ϵ�ĺ������루��Ҫ��֤������
����ͼ1������BCA=90�㣬�Ϧ�=90�㣬��BE_____CF�� EF_____|BE-AF|���>������<����=������
����ͼ2����0�㣼��BCA��180�㣬������һ�����ڡϦ����BCA��ϵ������_____��ʹ���е�����������Ȼ��������֤���������۳�����
����ͼ3����ֱ��CD������BCA���ⲿ���Ϧ�=��BCA�������EF��BE��AF�����߶�������ϵ�ĺ������루��Ҫ��֤������
�⣺��1����=��=��
������������ǣ��Ϧ�+��BCA=180�㣬
֤�����ڡ�BCE�У���CBE+��BCE=180��-��BEC=180��-�Ϧ���
�ߡ�BCA=180��-�Ϧ���
���CBE+��BCE=��BCA��
�֡� ��
��
�� ��
��
�֡�BC=CA����BEC=��CFA��
�� ��
��
��BE=CF��CE=AF��
�֡�EF=CF-CE��
��EF=|BE-AF|��
��2��EF=BE+AF��
������������ǣ��Ϧ�+��BCA=180�㣬
֤�����ڡ�BCE�У���CBE+��BCE=180��-��BEC=180��-�Ϧ���
�ߡ�BCA=180��-�Ϧ���
���CBE+��BCE=��BCA��
�֡�
 ��
����
 ��
���֡�BC=CA����BEC=��CFA��
��
 ��
����BE=CF��CE=AF��
�֡�EF=CF-CE��
��EF=|BE-AF|��
��2��EF=BE+AF��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ