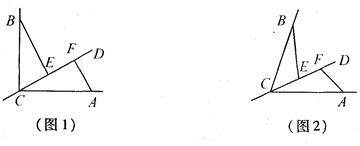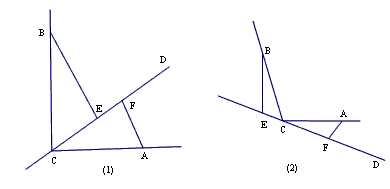Question

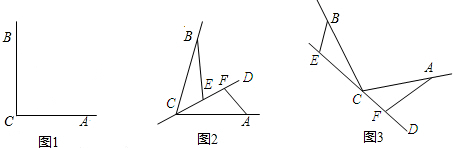
28、CD是经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α．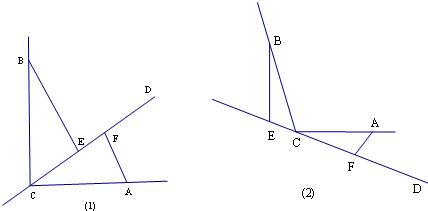
（1）如图（1），若直线CD经过∠BCA的内部，且E、F在射线CD上，当∠BCA=∠α=90°时，线段BE与CF有怎样的大小关系？并说明理由．
（2）如图（2），若直线CD经过∠BCA的外部，当∠BCA=∠α＞90°时，则EF、BE、AF三条线段之间有怎样的数量关系？并说明理由．

Answer 1

分析：（1）根据“AAS”可以证明Rt△BCE≌Rt△CAF，则BE=CF；
（2）同理证明Rt△BCE≌Rt△CAF，则CE=AF，BE=CF，可得EF=CE+CF=AF+BE．

解答：解：（1）BE=CF，理由：
∵∠BCE+∠ACF=90°，∠FCA+∠ACF=90°，
∴∠BCE=∠FCA，（同角的余角相等）
∵∠BEC=∠CFA，CA=CB，
∴Rt△BCE≌Rt△CAF（AAS），
∴BE=CF；

（2）EF=AF+BE，理由：
∵∠BCE+∠ACF=180°-∠α，∠FCA+∠ACF=180°-∠α，
∴∠BCE=∠FCA，（同角的补角相等）
∵∠BEC=∠CFA，CA=CB，
∴Rt△BCE≌Rt△CAF（AAS），
∴CE=AF，BE=CF，
∴EF=CE+CF=AF+BE．

点评：此题考查了两直角三角形全等的判定方法，是从特殊到一般，所用方法一样，依据有所不同．