题目内容
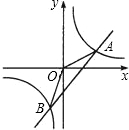 如图所示,反比例函数y=
如图所示,反比例函数y=| 1 | x |
(1)求A,B两点坐标;
(2)求S△AOB.
分析:(1)求两图象交点坐标,可把两个解析式归纳为一个方程组,解方程组的结果,即为交点坐标.
(2),在(1)的基础上,求出直线x轴或y轴的交点,把原三角形分成两个三角形,利用求和的方法,进行解答.
(2),在(1)的基础上,求出直线x轴或y轴的交点,把原三角形分成两个三角形,利用求和的方法,进行解答.
解答:解:(1)解方程组,得
=2x-1
2x2-x-1=0
∴x1=1,x2=-
A(1,1),B(-
,-2).
(2)设y=2x-1与x,y轴交于C,D,则C(
,0),D(0,-1)
∴S△AOB=S△OCA+S△BOD+S△OCD=
×
×1+
×1×
+
×
×1=
.
[解题技巧]运用方程组求点的坐标,由坐标再求面积.
| 1 |
| x |
2x2-x-1=0
∴x1=1,x2=-
| 1 |
| 2 |
A(1,1),B(-
| 1 |
| 2 |
(2)设y=2x-1与x,y轴交于C,D,则C(
| 1 |
| 2 |
∴S△AOB=S△OCA+S△BOD+S△OCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
[解题技巧]运用方程组求点的坐标,由坐标再求面积.
点评:此题主要考查利用解析式求交点坐标,只需列方程组解答即可.同学们要掌握解方程组的方法.

练习册系列答案
相关题目
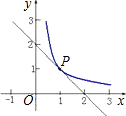 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y= (2013•石峰区模拟)如图所示,反比例函数
(2013•石峰区模拟)如图所示,反比例函数 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为
如图所示,反比例函数图象上一点A,过A作AB⊥x轴于B,若S△AOB=3,则反比例函数的解析式为