题目内容
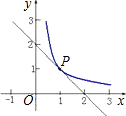 已知:如图所示,反比例函数y=
已知:如图所示,反比例函数y=| 1 |
| x |
(1)若反比例函数y=-
| k |
| x |
(2)设(1)问结论中的直线与x轴、y轴分别交于A、B两点.将∠ABO沿折痕AB翻折,设翻折后的OB边与x轴交于点C.
①直接写出点C的坐标;
②在经过A、B、C三点的抛物线的对称轴上是否存在一点P,使以P、O、M、C为顶点的四边形为梯形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)因为两函数只有一个公共点,将关于两个函数解析式的方程组转化为一元二次方程,令△=0即可求出k的值.进而求出两函数的解析式及M点的坐标.
(2)①根据直线解析式,先求出A、B两点坐标,再根据翻折变换的性质,得∠OBA=∠ABC,根据三角形内角平分线的性质定理,求出AC的长,易得C点坐标.
②由于A、C在x轴上,且A、C关于抛物线对称轴对称,可求出抛物线对称轴方程,根据P点的移动情况,可见有三种情况:一、当MP∥OC时,可根据M点纵坐标得到P点纵坐标;二、MO∥CP时,可根据直线MO的系数求出直线CP的系数,再将C点坐标代入,即可求得PC解析式,将对称轴坐标代入解析式,即可求得P点坐标;三、可根据直线MC的系数求出直线CP的系数,由于OP过原点,即可求得OP解析式,将对称轴坐标代入解析式,即可求得P点坐标.
(2)①根据直线解析式,先求出A、B两点坐标,再根据翻折变换的性质,得∠OBA=∠ABC,根据三角形内角平分线的性质定理,求出AC的长,易得C点坐标.
②由于A、C在x轴上,且A、C关于抛物线对称轴对称,可求出抛物线对称轴方程,根据P点的移动情况,可见有三种情况:一、当MP∥OC时,可根据M点纵坐标得到P点纵坐标;二、MO∥CP时,可根据直线MO的系数求出直线CP的系数,再将C点坐标代入,即可求得PC解析式,将对称轴坐标代入解析式,即可求得P点坐标;三、可根据直线MC的系数求出直线CP的系数,由于OP过原点,即可求得OP解析式,将对称轴坐标代入解析式,即可求得P点坐标.
解答:解:(1)因为反比例函数y=-
与直线y=kx+6只有一个公共点,
将y=-
代入y=kx+6得
kx2+6x+k=0,
由△=36-4k2=0
得k=±3.
又∵k<0,
∴k=-3.
∴两个函数的解析式分别为y=
,和y=-3x+6.
∴点M的坐标为(1,3).(2分)
(2)①如图,y=-3x+6与x轴、y轴两交点A、B的坐标分别为(2,0),(0,6).
根据翻折不变性,∠OBA=∠ABC,
设AC=a,根据勾股定理,BC=
,
根据三角形内角平分线性质定理,
=
,
解得a=
或a=-2(负值舍去),
于是OC=2+
=
,可求得点C的坐标为(
,0).(3分)
②存在点P满足四边形POMC为梯形.(4分)
又∵经过点A、B、C三点的抛物线的对称轴为x=
.(5分)
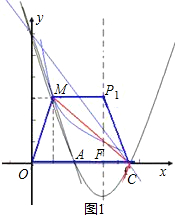
一、当MP1∥OC时,P1点的纵坐标为M点的纵坐标3,则P1点的纵坐标为(
,3),而此时OM与CP1不平行.
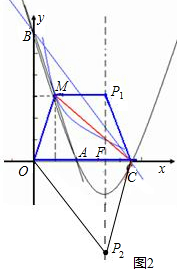
二、当MO∥CP2时,由于OM解析式为y=3x,设P2C解析式为y=3x+b,
将C(
,0)代入解析式
可得b=-
,
则P2C解析式为y=3x-
,
当x=
时,y=-
,
则P2点的坐标为(
,-
),
经判断,OP2与MC不平行.(6分)
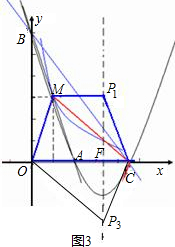
三、当MC∥OP3时,由于CM解析式为y=-
x+
,则P3O解析式为y=-
x,
当x=
时,y=-
,则P3点的坐标为(
,-
),
经判断,MO与CP不平行.(7分)
∴满足条件的P点的坐标为(
,3)、(
,-
)和(
,-
).
| k |
| x |
将y=-
| k |
| x |
kx2+6x+k=0,
由△=36-4k2=0
得k=±3.
又∵k<0,
∴k=-3.
∴两个函数的解析式分别为y=
| 3 |
| x |
∴点M的坐标为(1,3).(2分)
(2)①如图,y=-3x+6与x轴、y轴两交点A、B的坐标分别为(2,0),(0,6).
根据翻折不变性,∠OBA=∠ABC,
设AC=a,根据勾股定理,BC=
| 62+(2+a)2 |
根据三角形内角平分线性质定理,
| ||
| a |
| 6 |
| 2 |
解得a=
| 5 |
| 2 |
于是OC=2+
| 5 |
| 2 |
=
| 9 |
| 2 |
| 9 |
| 2 |
②存在点P满足四边形POMC为梯形.(4分)
又∵经过点A、B、C三点的抛物线的对称轴为x=
| 13 |
| 4 |
一、当MP1∥OC时,P1点的纵坐标为M点的纵坐标3,则P1点的纵坐标为(
| 13 |
| 4 |
二、当MO∥CP2时,由于OM解析式为y=3x,设P2C解析式为y=3x+b,
将C(
| 9 |
| 2 |
可得b=-
| 27 |
| 2 |
则P2C解析式为y=3x-
| 27 |
| 2 |
当x=
| 13 |
| 4 |
| 15 |
| 4 |
则P2点的坐标为(
| 13 |
| 4 |
| 15 |
| 4 |
经判断,OP2与MC不平行.(6分)
三、当MC∥OP3时,由于CM解析式为y=-
| 6 |
| 7 |
| 27 |
| 7 |
| 6 |
| 7 |
当x=
| 13 |
| 4 |
| 39 |
| 14 |
| 13 |
| 4 |
| 39 |
| 14 |
经判断,MO与CP不平行.(7分)
∴满足条件的P点的坐标为(
| 13 |
| 4 |
| 13 |
| 4 |
| 15 |
| 4 |
| 13 |
| 4 |
| 39 |
| 14 |



点评:此题考查了一次函数、二次函数及反比例函数的性质,函数解析式组成的方程组的解的个数和函数图象交点个数及根的判别式的关系.尤其是(3),结合梯形的性质和抛物线的性质,考查了点的存在性问题,要利用图形进行分类讨论.

练习册系列答案
相关题目
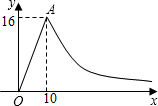 药量为16mg.根据以上信息解答下列问题:
药量为16mg.根据以上信息解答下列问题:


 自变量x的取值范围是 。药物燃烧完后,
自变量x的取值范围是 。药物燃烧完后, 
 自变量x的取值范围是
。药物燃烧完后,
自变量x的取值范围是
。药物燃烧完后,
