题目内容
二次函数y=ax2+bx+c的图象如图所示，反比例函数y=| ac |
| x |
分析：首先根据二次函数图象的开口方向确定a＜0，再根据对称轴在y轴左，可确定a与b同号，然后再根据二次函数与y轴的交点可以确定c＞0，再根据反比例函数的性质和正比例函数的性质确定出两个函数图象所在象限，进而得到答案．
解答：解：∵抛物线开口向下，
∴a＜0，
∵对称轴在y轴左，
∴a与b同号，
∴b＜0，
∵抛物线与y轴交于正半轴，
∴c＞0，
∴ac＜0，
∴反比例函数y=
在二四象限，
∵b＜0，
∴正比例函数y=bx的图象经过原点，且在二四象限，
故选：B．
∴a＜0，
∵对称轴在y轴左，
∴a与b同号，
∴b＜0，
∵抛物线与y轴交于正半轴，
∴c＞0，
∴ac＜0，
∴反比例函数y=
| ac |
| x |
∵b＜0，
∴正比例函数y=bx的图象经过原点，且在二四象限，
故选：B．
点评：此题主要考查了二次函数图象与系数的关系，以及正比例函数与反比例函数的性质，关键是正确判断出a、b、c的符号．
练习册系列答案
相关题目
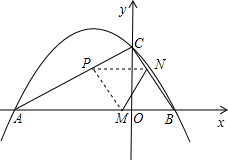点C
如图为二次函数y=ax2+bx+c（a≠0）的图象，则下列说法：①abc＞0；②2a+b=0；③a+b+c＞0；④当-1＜x＜3时，y＞0．其中正确结论的序号是
（2012•孝感）二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示．对于下列说法：