题目内容
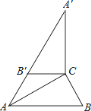
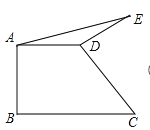
【题目】如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,求BC的长.
【答案】5
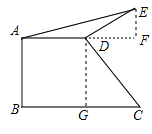
【解析】试题分析:过D点作DG⊥BC,垂足为G,过E点作EF⊥AD,交AD的延长线与F点,由旋转的性质可知△CDG≌△EDF,从而有EF=CG,由△ADE的面积可求EF,得出CG的长,由矩形的性质得BG=AD,根据BC=BG+GC求解.
试题解析:
解:如图,作DG⊥BC于G,作EF⊥AD于F.得矩形ABGD,则BG=AD=2.
∵△ADE的面积为3.
∴EF=3.
根据旋转的性质,可知DE=DC,
∵∠CDG+∠FDC =∠EDF+∠CDF =90°,
∴∠GDC =∠EDF,又∠DGC =∠F =90°,
∴△CDG≌△EDF.
∴EF=GC=3,
∴BC=BG+GC=2+3=5.

练习册系列答案
相关题目