题目内容
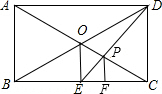 在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连接DE交AC于点P,过P作PF⊥BC,垂足为F,则
在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC,垂足为E,连接DE交AC于点P,过P作PF⊥BC,垂足为F,则| CF | CB |
分析:根据题意易证△OBE∽△DBC和△EPF∽△EDC,利用相似三角形的相似比求解.
解答:解:∵OB=OD=
BD,OE⊥BC,CD⊥BC,
∴△OBE∽△DBC,
∴OE:CD=1:2,
∵OE∥CD,
∴△OEP∽△CDP,
∴
=
,
∵PF∥DC,
∴△EPF∽△EDC,
∴
=
,
∵CE=
BC,
∴
=
.
故答案为
.
| 1 |
| 2 |
∴△OBE∽△DBC,
∴OE:CD=1:2,
∵OE∥CD,
∴△OEP∽△CDP,
∴
| EP |
| PD |
| 1 |
| 2 |
∵PF∥DC,
∴△EPF∽△EDC,
∴
| CF |
| CE |
| 2 |
| 3 |
∵CE=
| 1 |
| 2 |
∴
| CF |
| CB |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:本题考查对相似三角形性质的理解.相似三角形对应边的比相等.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 ,或许对你有所帮助哦!
,或许对你有所帮助哦!

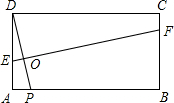
 如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折,然后放在桌面上,折叠后所成的图形覆盖桌面的面积是
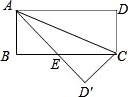
如图,在矩形ABCD中,AB=5,BC=12,将矩形ABCD沿对角线对折,然后放在桌面上,折叠后所成的图形覆盖桌面的面积是 在矩形ABCD中,△ABD沿对角线BD对折,A与A′重合,AD=8,AB=6,A′D与BC相交于O.
在矩形ABCD中,△ABD沿对角线BD对折,A与A′重合,AD=8,AB=6,A′D与BC相交于O.