题目内容
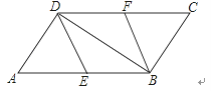
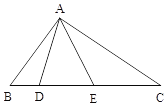
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
【答案】(1)45°;(2)∠DAE=30°;(3)α+2β=180.
【解析】
(1)由题意得出∠BEA=![]() ,∠CDA =
,∠CDA =![]() ,再在△ADE中
,再在△ADE中
利用内角和等于180°即可.
(2)同(1)理可快速得出答案.
(3)综合(1)(2)可总结出α与β的之间数量关系.
(1)∵AB=BE ,AC=CD
∴∠BEA=![]() ,∠CDA =
,∠CDA =![]()
在△ADE中
∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )=
(180°∠BAC )=![]() ×(180°90°)=45°
×(180°90°)=45°
(2)∠DAE=30°
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )= 30°
(180°∠BAC )= 30°
(3)α+2β=180
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )
(180°∠BAC )
∠DAE=![]() (180°∠BAC )
(180°∠BAC )
α+2β=180.

练习册系列答案
相关题目