题目内容
平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q。
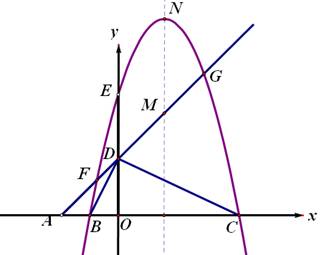
1.求经过B、E、C三点的抛物线的解析式;
2.判断⊿BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标
3.若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由。
1.B(-1,0) E(0,4) C(4,0) 设解析式是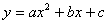
可得  解得
解得 (2分)
∴
(2分)
∴
2.⊿BDC是直角三角形 (1分)
∵BD2=BO2+DO2=5 , DC2=DO2+CO2=20 ,BC2=(BO+CO)2=25
∴BD2+ DC2= BC2 (1分)
∴⊿BDC是Rt⊿
点A坐标是(-2,0),点D坐标是(0,2)直线AD的解析式是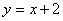 (1分)
(1分)
设点P坐标是(x,x+2)
当OP=OC时 x2+(x+2)2=16
解得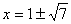 (
(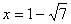 不符合,舍去)此时点P(
不符合,舍去)此时点P(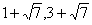 )
)
当PC=OC时 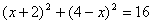 方程无解
方程无解
当PO=PC时,点P在OC的中垂线上,∴点P横坐标是2, 得点P坐标是(2,4)
∴当⊿POC是等腰三角形时,点P坐标是(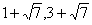 )或(2,4) (2分)
)或(2,4) (2分)
(1) 3.点M坐标是(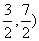 )N坐标是(
)N坐标是(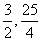 )∴MN=
)∴MN=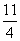
设点P 为(x,x+2)Q(x,-x2+3x+4),则PQ=
①若PQNM是菱形,则PQ=MN,可得x1=0.5 x2=1.5
当x2=1.5时,点P与点M重合;当x1=0.5时,可求得PM=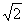 ,所以菱形不存在(2分)
,所以菱形不存在(2分)
②能成为等腰梯形,此时点P的坐标是(2.5,4.5)(2分)
【解析】略

 阅读快车系列答案
阅读快车系列答案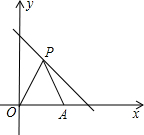 如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6上的点,点A坐标是(5,0),O是坐标原点,△PAO的面积为m,则m关于x的函数关系式是
如图,在平面直角坐标系中,点P(x,y)是第一象限直线y=-x+6上的点,点A坐标是(5,0),O是坐标原点,△PAO的面积为m,则m关于x的函数关系式是 如图,在平面直角坐标系中,点A是抛物线y=a(x+2)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )
如图,在平面直角坐标系中,点A是抛物线y=a(x+2)2+k与y轴的交点,点B是这条抛物线上的另一点,且AB∥x轴,则以AB为边的等边三角形ABC的周长为( )