Question

抛物线y=ax²+bx+c与y轴交于点C（0，-2），与直线y=x交于点A（-2，-2），B（2，2）．
（1）求抛物线的解析式；
（2）如图，线段MN在线段AB上移动（点M与点A不重合，点N与点B不重合），且MN=

2

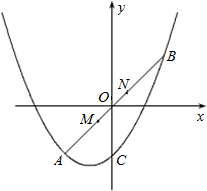，若M点的横坐标为m，过点M作x轴的垂线与x轴交于点P，过点N作x轴的垂线与抛物线交于点Q．以点P，M，Q，N为顶点的四边形能否为平行四边形？若能，请求出m的值；若不能，请说明理由．

Answer 1

分析：（1）把C的坐标代入求出c的值，把A、B的坐标代入抛物线的解析式得到方程组，求出方程组的解即可求出抛物线的解析式；
（2）以点P，M，Q，N为顶点的四边形能为平行四边形，当M在OA上，N在OB上时，以点P，M，Q，N为顶点的四边形为平行四边形，求出N的横坐标，求出NH、MH，根据勾股定理求出m即可．

解答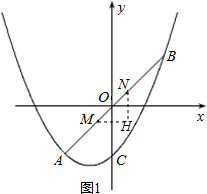：解：（1）∵抛物线y=ax²+bx+c与y轴交于点C（0，-2），
代入得：c=-2，
∴y=ax²+bx-2，
把A（-2，-2），B（2，2）代入得：

-2=4a-2b-2 2=4a+2b-2

，
解得：

a= 1 2 b=1

，
∴y=

1

2

x²+x-2，
答：抛物线的解析式是y=

1

2

x²+x-2．

（2）∵MN=

2

，点A，B都在直线y=x上，MN在直线AB上，MN在线段 AB上，M的横坐标为m．
如图1，过点M作x轴的平行线，过点N作y轴的平行线，它们相交于点H．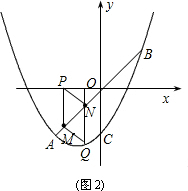
∴△MHN是等腰直角三角形．
∴MH=NH=1．
∴点N的坐标为（m+1，m+1）
①如图2，当m＜0时，PM=-m，
NQ=m+1-[

1

2

（m+1）²+m+1-2]=-

1

2

（m+1）²+2．
当四边形PMQN为平行四边形时，PM=NQ．
∴-m=-

1

2

（m+1）²+2．
解得：m=

3

（不合题意舍去）或-

3

，
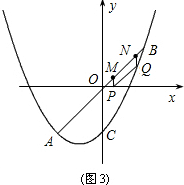
②如图3，当m＞0，PM=m，
NQ=m+1-[

1

2

（m+1）²+m+1-2]=-

1

2

（m+1）²+2．
当四边形PMQN为平行四边形时，PM=NQ．
∴m=-

1

2

（m+1）²+2．
解得：m=-2-

7

（不合题意舍去）或

7

-2，
③∵直线AB过O，即直线经过第一、三象限，
∴点M在第3象限点N在第1象限不存在；
∴当m=-

3

或m=

7

-2时，以点P，M，Q，N为顶点的四边形能为平行四边形．

点评：本题主要考查对一次函数的性质，用待定系数法求二次函数的解析式，解二元一次方程组，平行四边形的性质，勾股定理等知识点的理解和掌握，能用待定系数法求二次函数的解析式和得到MD=ND=|2m|是解此题的关键．