题目内容
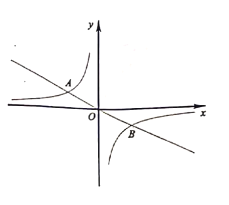
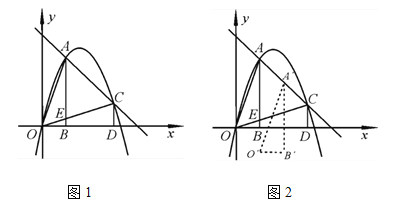
【题目】如图1,已知抛物线y=ax2+bx上有两点A、C,分别过A、C作x轴的垂线,垂足分别为点B、点D,OC与AB相交于点E.已知点A(1,3),且△AOB≌△OCD.
(1)求此抛物线的解析式;
(2)点P为线段OC上一动点,过点P作x轴的垂线交抛物线于点F,当四边形AEPF为平行四边形时,求点P坐标;
(3)如图2,若△AOB沿AC方向由A→C平移得到△A′O′B′,在平移过程中,△AOB与△OCD的重叠部分的面积记为S,试探究S是否存在最大值?若存在,求出A′的坐标;若不存在,请说明理由.
【答案】(1) y=![]() x 2+
x 2+![]() x; (2) (2,
x; (2) (2,![]() ) ;(3)见解析.
) ;(3)见解析.
【解析】分析:(1)由全等三角形的性质得到OB=CD,AB=OD.即可得到C的坐标,把A、C的坐标代入,解方程即可得到结论;
(2)设直线OC的解析式为:y=kx,把C的坐标代入即可得到k的值,从而得到E的坐标.设点P(m,![]() m),则F(m,
m),则F(m,![]() m2+
m2+![]() m ) .要使四边形AEPF为平行四边形 ,则AE=PF ,解方程即可得到结论;
m ) .要使四边形AEPF为平行四边形 ,则AE=PF ,解方程即可得到结论;
(3)设A′B′交x轴于T,交OC于Q,A′O′交x轴于K,交OC于R.求得直线AC的解析式为y=-x+4,可设点A′的横坐标为t,则点A′(t,-t +4 ),点Q的坐标为(t,![]() ) .
) .
过点R作RF⊥A′B′于点F,由相似三角形的性质可求出RF的长,由△A′KT∽△A′O′B′可求出KT的长,进而得到A′Q的长,由S四边形RKTQ=S△A′KT-S△A′RQ得到S是关于t的二次函数,配方即可得出结论.
详解:(1)∵△AOB≌△OCD,∴OB=CD,AB=OD.
∵A(1,3),∴C(3,1),
∴![]() ,
,
解得:a=![]() ,b=
,b=![]() ,∴抛物线的解析式为y=
,∴抛物线的解析式为y=![]() x 2+
x 2+![]() x,
x,
(2)设直线OC的解析式为:y=kx,则1=3k ,∴k=![]() ,∴E(1,
,∴E(1,![]() ).
).
设点P(m,![]() m),则F(m,
m),则F(m,![]() m2+
m2+![]() m ) .
m ) .
要使四边形AEPF为平行四边形 ,则AE=PF ∴3-![]() =
=![]() m2+
m2+![]() m-
m-![]() m,
m,
∴m=1(不合题意,舍去)或m=2 ∴P(2,![]() ),∴当四边形AEPF为平行四边形时,P点的坐标为(2,
),∴当四边形AEPF为平行四边形时,P点的坐标为(2,![]() ).
).
(3)设A′B′交x轴于T,交OC于Q,A′O′交x轴于K,交OC于R.求得直线AC的解析式为y=-x+4,可设点A′的横坐标为t,则点A′(t,-t +4 ),∴点Q的坐标为(t,![]() ) .
) .
过点R作RF⊥A′B′于点F.
∵△A′RQ∽△AOE,∴![]() ,∴RF=
,∴RF=![]() =
=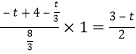 ,
,
由△A′KT∽△A′O′B′得![]() ,∴KT=
,∴KT=![]() A′T=
A′T=![]() (4-t),A′Q=(-t+4)-
(4-t),A′Q=(-t+4)-![]() =
=![]() ,
,
∴S四边形RKTQ=S△A′KT-S△A′RQ=![]() KT·A′T-
KT·A′T-![]() A′Q·RF=
A′Q·RF=![]() ·(4-t)-
·(4-t)-![]() ·
·![]() ,
,
=![]() =
=![]() ,∴当t=2时,S最大,∴A′(2,2) .
,∴当t=2时,S最大,∴A′(2,2) .

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案