题目内容
【题目】求解：已知：如图1，P为△ADC内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD。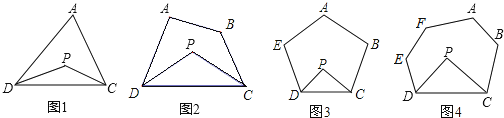
（1）如果∠A=60°，那么∠P是多少度；如果∠A=90°，那么∠P是多少度；如果∠A=x°，则∠P是多少度？
（2）如图2，P为四边形ABCD内一点，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A+∠B的数量关系，并写出你的探索过程；
（3）如图3，P为五边形ABCDE内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E的数量关系。
（4）如图4，P为六边形ABCDEF内一点，DP、CP分别平分DP、CP分别平分∠ADC和∠ACD，请直接写出∠P与∠A+∠B+∠E+∠F的数量关系。
（5）若P为n边形A1A2A3…An内一点，PA1平分∠AnA1A2 ， PA2平分∠A1A2A3 ， 请直接写出∠P与∠A3+A4+A5+…∠An的数量关系。（用含n的代数式表示）
【答案】
（1）
解答：∵DP、CP分别平分∠ADC和∠ACD，
∴∠PDC= 
∠ADC，∠PCD= ∠ACD，
∴∠DPC=180°-∠PDC-∠PCD=180°- （∠ADC+∠ACD）=180°- （180°-∠A）
=90°+ ∠A，
∴如果∠A=60°，那么∠P=120°；如果∠A=90°，那么∠P=135°；如果∠A=x°，则∠P=（90+ 
）°
（2）
解答： ∵DP、CP分别平分∠ADC和∠BCD，
∴∠PDC= ∠ADC，∠PCD= ∠BCD，
∴∠DPC=180°-∠PDC-∠PCD=180°- （∠ADC+∠BCD）=180°- （360°-∠A-∠B）
= （∠A+∠B）；
（3）
解答：五边形ABCDEF的内角和为：（5-2）180°=540°，
∵DP、CP分别平分∠EDC和∠BCD，
∴∠P= ∠EDC，∠PCD= ∠BCD，
∴∠P=180°-∠PDC-∠PCD=180°- （∠EDC+∠BCD）=180°- （540°-∠A-∠B-∠E）
= （∠A+∠B+∠E）-90°．
（4）
解答：六边形ABCDEF的内角和为：（6-2）180°=720°，
∵DP、CP分别平分∠EDC和∠BCD，
∴∠PDC= ∠EDC，∠PCD= ∠BCD，
∴∠P=180°-∠PDC-∠PCD=180°- （∠EDC+∠BCD）=180°- （720°-∠A-∠B-∠E-∠F）= （∠A+∠B+∠E+∠F）-180°．
（5）
解答：同第一小题可得，∠P= （∠A3+∠A4+∠A5+…∠An）-（n-4）×90°.
【解析】这五小题的做法类似，把求∠P的度数转换成求 （∠EDC+∠BCD），由多边形的内角和可得（∠EDC+∠BCD）与其他内角和的数量关系，从而得∠P.
【考点精析】认真审题，首先需要了解多边形内角与外角(多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°)．
