题目内容
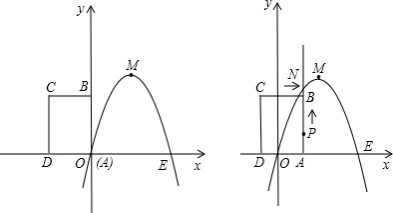
如图,已知抛物线经过坐标原点O及A(-2
,0),其顶点为B(m,3),C是A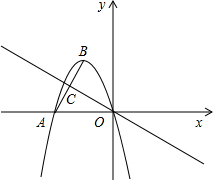 B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
(1)求此抛物线及直线OC的解析式;
(2)当点E运动到抛物线上时,求BD的长;
(3)连接AD,当点E运动到何处时,△AED的面积为
?请直接写出此时E点的坐标.
| 3 |
 B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.(1)求此抛物线及直线OC的解析式;
(2)当点E运动到抛物线上时,求BD的长;
(3)连接AD,当点E运动到何处时,△AED的面积为
3
| ||
| 4 |
分析:(1)先根据抛物线过原点和A(-2
, 0),得出抛物线对称轴为x=-
,故可得出B点坐标,设抛物线的解析式为y=a(x+
)2+3,由抛物线经过(0,0)可求出a的值,故可得出抛物线的解析式,
由C为AB的中点可得出C点坐标,进而得出直线OC的解析式;
(2)连接ED,由于点E是抛物线与直线OC的交点所以联立二次函数与直线的解析式可求出E点坐标,过E作EF⊥y轴于F可求出OF的长,再由EO=ED可得出D点坐标,故可求出BD的长.
(3)连接DE、AE、AD,设E(x,-
x),由A,D两点坐标即可得出OA=2
,OD=
,由S四边形AODE=S△AOE+S△DOE=S△AED+S△AOD即可得出结论.
| 3 |
| 3 |
| 3 |
由C为AB的中点可得出C点坐标,进而得出直线OC的解析式;
(2)连接ED,由于点E是抛物线与直线OC的交点所以联立二次函数与直线的解析式可求出E点坐标,过E作EF⊥y轴于F可求出OF的长,再由EO=ED可得出D点坐标,故可求出BD的长.
(3)连接DE、AE、AD,设E(x,-
| ||
| 3 |
| 3 |
| 10 |
| 3 |
解答:解:(1)∵抛物线过原点和A(-2
, 0),
∴抛物线对称轴为x=-
.
∴B(-
, 3).
设抛物线的解析式为y=a(x+
)2+3.
∵抛物线经过(0,0),
∴0=3a+3.
∴a=-1.
∴y=-(x+
)2+3,
=-x2-2
x.
∵C为AB的中点,A(-2
,0)、B(-
,3),
∴C(-
,
).
∴直线OC的解析式为y=-
x;
(2)如图1,连接ED.
∵点E为抛物线y=-x2-2
x与直线y=-
x的交点(点E与点O不重合).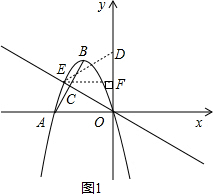
∴
,解得
或
(不合题意,舍去),
∴E(-
,
);
过E作EF⊥y轴于F,可得OF=
,
∵OE=DE,EF⊥y轴,
∴OF=DF,
∴DO=2OF=
,
∴D(0,
),
∴BD=
=
;
(3)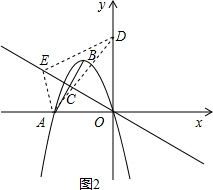 如图2,连接DE、AE、AD,设E(-a,
如图2,连接DE、AE、AD,设E(-a,
a)(a>0),
∵A(-2
,0),D(0,
a),
∴OA=2
,OD=
a,
∴S△AED=S△AOE+S△DOE-S△AOD=
×2
×
a+
×a×
a-
×2
×
a=
a2-a,
∴
a2-a=
,
解得a=
;
∴E(-
,
),
同理,当E在第四象限时,
E(
,-
).
故E点的坐标为(-
,
)或(
,-
).
| 3 |
∴抛物线对称轴为x=-
| 3 |
∴B(-
| 3 |
设抛物线的解析式为y=a(x+
| 3 |
∵抛物线经过(0,0),
∴0=3a+3.
∴a=-1.
∴y=-(x+
| 3 |
=-x2-2
| 3 |
∵C为AB的中点,A(-2
| 3 |
| 3 |
∴C(-
3
| ||
| 2 |
| 3 |
| 2 |
∴直线OC的解析式为y=-
| ||
| 3 |
(2)如图1,连接ED.
∵点E为抛物线y=-x2-2
| 3 |
| ||
| 3 |

∴
|
|
|
∴E(-
5
| ||
| 3 |
| 5 |
| 3 |
过E作EF⊥y轴于F,可得OF=
| 5 |
| 3 |
∵OE=DE,EF⊥y轴,
∴OF=DF,
∴DO=2OF=
| 10 |
| 3 |
∴D(0,
| 10 |
| 3 |
∴BD=
(
|
2
| ||
| 3 |
(3)
 如图2,连接DE、AE、AD,设E(-a,
如图2,连接DE、AE、AD,设E(-a,
| ||
| 3 |
∵A(-2
| 3 |
2
| ||
| 3 |
∴OA=2
| 3 |
2
| ||
| 3 |
∴S△AED=S△AOE+S△DOE-S△AOD=
| 1 |
| 2 |
| 3 |
| ||
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
| ||
| 3 |
∴
| ||
| 3 |
3
| ||
| 4 |
解得a=
3
| ||
| 2 |
∴E(-
3
| ||
| 2 |
| 3 |
| 2 |
同理,当E在第四象限时,
E(
| ||
| 2 |
| 1 |
| 2 |
故E点的坐标为(-
3
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、三角形的面积公式等知识,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
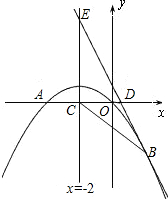 2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E.
2x+1经过抛物线上一点B(2,m),且与y轴.直线x=-2分别交于点D、E. (2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.
(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=-1.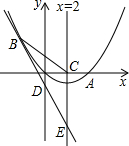 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E,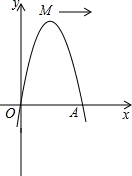 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),