题目内容
如图，⊙O中，弦AB的长为2，OC⊥AB于C，OC=1，若从⊙O外一点P作⊙O的两条切线，切点分别为A、B，则∠APB的度数为
- A.120°
- B.90°
- C.60°
- D.45°
B
分析：连OA，OB．根据已知条件运用切线的性质证明四边形AOBP是正方形．
解答：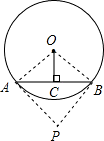
解：连OA，OB．
PA，PB是切线，则∠OAP=∠OBP=90°．
OC⊥AB?AC=BC=1=OC?△ACO，△BCO是等腰直角三角形?∠AOB=90°?四边形AOBP是正方形?∠APB=90°．
故选B．
点评：本题利用了切线的性质：圆的切线垂直于经过切点的半径，
等腰直角三角形的判定和性质，正方形的判定和性质求解．
分析：连OA，OB．根据已知条件运用切线的性质证明四边形AOBP是正方形．
解答：
解：连OA，OB．PA，PB是切线，则∠OAP=∠OBP=90°．
OC⊥AB?AC=BC=1=OC?△ACO，△BCO是等腰直角三角形?∠AOB=90°?四边形AOBP是正方形?∠APB=90°．
故选B．
点评：本题利用了切线的性质：圆的切线垂直于经过切点的半径，
等腰直角三角形的判定和性质，正方形的判定和性质求解．
练习册系列答案
相关题目
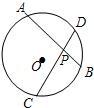10、如图，⊙O中，弦AB和CD相交于P，CP=2.5，PD=6，AB=8，那么以AP、PB的长为两根的一元二次方程是（ ）
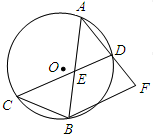如图，⊙O中，弦AB、CD相交于AB的中点E，连接AD并延长至点F，使DF=AD，连接BC、BF．
（2013•毕节地区）如图在⊙O中，弦AB=8，OC⊥AB，垂足为C，且OC=3，则⊙O的半径（ ）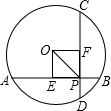
如图，⊙O中，弦AB，CD相交于P，且四边形OEPF是正方形，连接OP．若⊙O的半径为5cm，
如图，⊙O中，弦AB⊥CD于点E．若ON⊥BD于N，求证：ON=