题目内容
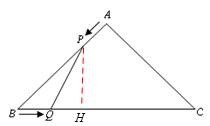
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2.
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
(1)当t=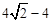 或
或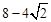 时,△PBQ是直角三角形;(2)①y=8-
时,△PBQ是直角三角形;(2)①y=8-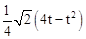 (0≤t≤4),②当t=2时,y取得最小值,最小值是
(0≤t≤4),②当t=2时,y取得最小值,最小值是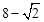 ;(3)y
;(3)y .
.
解析试题分析:(1)分∠PQB=90°和∠QPB=90°两种情况讨论即可;
(2)根据三角形的面积公式列式y=S△ABC-S△BPQ即得函数关系式,根据二次函数最值原理即可得出y取得最小值时t的值和y的最小值;
(3)把t2-4 t=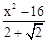 代入y=8-
代入y=8-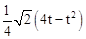 化简即可.
化简即可.
试题解析:(1)当t=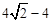 或
或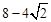 时,△PBQ是直角三角形,理由如下:
时,△PBQ是直角三角形,理由如下:
∵BQ=AP=t, BP=4-t,
∴①当∠PQB=90°时,由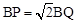 得:
得: t =4-t,解得:t=
t =4-t,解得:t=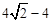 ;
;
②当∠QPB=90°时,由 得:
得: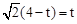 ,解得:t=
,解得:t=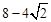 .
.
∴当t=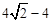 或
或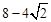 时,△PBQ是直角三角形.
时,△PBQ是直角三角形.
(2)①过P作PH⊥BC,在Rt△PHB中,BP=4-t,PH=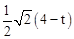 ,
,
∴S△BPQ=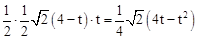 ,
,
∴y=S△ABC-S△BPQ=8-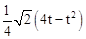 .
.
由题意可知:0≤t≤4.
②y=8-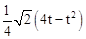 =
= ,
,
∴当t=2时,y取得最小值,最小值是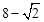 .
.
(3)在Rt△PQH中,PH=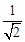 (4-t),HQ=
(4-t),HQ=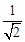 (4-t)-t,
(4-t)-t,
由PQ2= PH2+HQ2,则x2=〔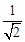 (4-t)〕2+〔
(4-t)〕2+〔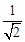 (4-t)-t〕2
(4-t)-t〕2
化简得:x2=(2+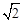 )t 2-4(2+
)t 2-4(2+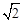 )t+16,∴ t2-4 t=
)t+16,∴ t2-4 t=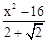 .
.
将t2-4t=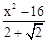 代入y=8-
代入y=8-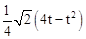 ,得y=8+
,得y=8+ ·
·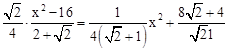 .
.
考点:1.双动点问题;2.由实际问题列函数关系式;3.二次函数的性质;4.直角三角形的判定;5.勾股定理;6.分类思想、转换思想和整体思想的应用.

 (b,c是常数,且c<0)与
(b,c是常数,且c<0)与 轴分别交于点A、B(点A位于点B的左侧),与
轴分别交于点A、B(点A位于点B的左侧),与 轴的负半轴交于点C,点A的坐标为(-1,0).
轴的负半轴交于点C,点A的坐标为(-1,0).
 .求抛物线的解析式.
.求抛物线的解析式. 与坐标轴交于
与坐标轴交于 三点,点
三点,点 的横坐标为
的横坐标为 ,过点
,过点 的直线
的直线 与
与 轴交于点
轴交于点 ,点
,点 是线段
是线段 上的一个动点,
上的一个动点, 于点
于点 .若
.若 ,且
,且 .
.
 的值
的值 的坐标(其中
的坐标(其中 用含
用含 的式子表示):
的式子表示): 为等腰三角形?
为等腰三角形? 元,每售出一个小家电可获得的利润是多少元?(用含
元,每售出一个小家电可获得的利润是多少元?(用含 元,此时的销售量是多少?(用含
元,此时的销售量是多少?(用含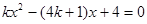 .
. 的图象与
的图象与 轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标;
轴两个交点的横坐标均为整数,且k为正整数,求k值并用配方法求出抛物线的顶点坐标; ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%. 的二次函数y=px2-(3p+2)x+2p+2(p>0)
的二次函数y=px2-(3p+2)x+2p+2(p>0)