题目内容
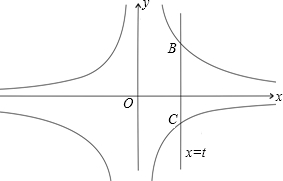 (2012•株洲)如图,直线x=t(t>0)与反比例函数y=
(2012•株洲)如图,直线x=t(t>0)与反比例函数y=| 2 |
| x |
| -1 |
| x |
分析:先分别求出B、C两点的坐标,得到BC的长度,再根据三角形的面积公式即可得出△ABC的面积.
解答:解:把x=t分别代入y=
,y=
,得y=
,y=-
,
所以B(t,
)、C(t,-
),
所以BC=
-(-
)=
.
∵A为y轴上的任意一点,
∴点A到直线BC的距离为t,
∴△ABC的面积=
×
×t=
.
故选C.
| 2 |
| x |
| -1 |
| x |
| 2 |
| t |
| 1 |
| t |
所以B(t,
| 2 |
| t |
| 1 |
| t |
所以BC=
| 2 |
| t |
| 1 |
| t |
| 3 |
| t |
∵A为y轴上的任意一点,
∴点A到直线BC的距离为t,
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
| t |
| 3 |
| 2 |
故选C.
点评:此题考查了反比例函数图象上点的坐标特征及三角形的面积,求出BC的长度是解答本题的关键,难度一般.

练习册系列答案
相关题目
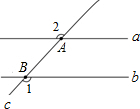 (2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )
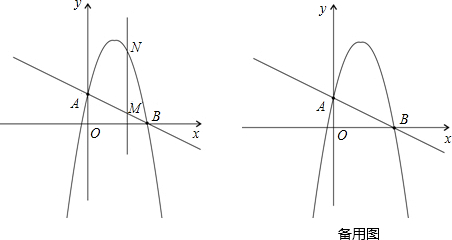
(2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( ) (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )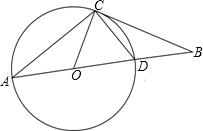 (2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.
(2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.