题目内容
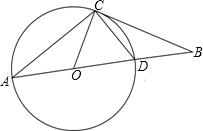 (2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.
(2012•株洲)如图,已知AD为⊙O的直径,B为AD延长线上一点,BC与⊙O切于C点,∠A=30°.求证:(1)BD=CD;
(2)△AOC≌△CDB.
分析:(1)由AD为⊙O的直径,根据直径对的圆周角是直角,即可得∠ACD=90°,又由∠A=30°,OA=OC=OD,利用等边对等角与三角形外角的性质,即可求得∠ACO=30°,∠ODC=∠OCD=60°,又由BC与⊙O切于C点,根据切线的性质,即可求得∠B=∠BCD=30°,由等角对等边,即可证得BD=CD;
(2)由(1)可知∠A=∠ACO=∠BCD=∠B=30°,即可得AC=BC,然后由ASA,即可证得△AOC≌△CDB.
(2)由(1)可知∠A=∠ACO=∠BCD=∠B=30°,即可得AC=BC,然后由ASA,即可证得△AOC≌△CDB.
解答:证明:(1)∵AD为⊙O的直径,
∴∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,-----------------------------(1分)
又∵BC与⊙o切于C,
∴∠OCB=90°,------------------------------------------(2分)
∴∠BCD=30°,
∴∠B=30°,
∴∠BCD=∠B,
∴BD=CD.--------------------------------------------(4分)
(2)∵∠A=∠ACO=∠BCD=∠B=30°,----------------------------(6分)
∴AC=BC,-----------------------------------------------(7分)
在△AOC和△BDC中,
∴△AOC≌△BDC(ASA).--------------------------------------------------------(8分)
∴∠ACD=90°,
又∵∠A=30°,OA=OC=OD,
∴∠ACO=30°,∠ODC=∠OCD=60°,-----------------------------(1分)
又∵BC与⊙o切于C,
∴∠OCB=90°,------------------------------------------(2分)
∴∠BCD=30°,
∴∠B=30°,
∴∠BCD=∠B,
∴BD=CD.--------------------------------------------(4分)
(2)∵∠A=∠ACO=∠BCD=∠B=30°,----------------------------(6分)
∴AC=BC,-----------------------------------------------(7分)
在△AOC和△BDC中,
|
∴△AOC≌△BDC(ASA).--------------------------------------------------------(8分)
点评:此题考查了切线的性质、等腰三角形的判定与性质以及全等三角形的判定.此题难度适中,注意数形结合思想的应用.

练习册系列答案
相关题目
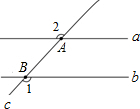 (2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( )
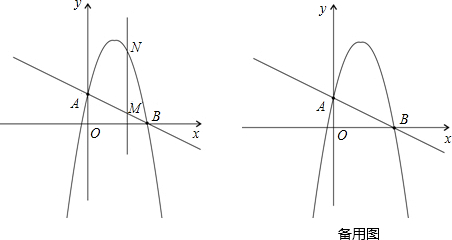
(2012•株洲)如图,已知直线a∥b,直线c与a、b分别交于A、B;且∠1=120°,则∠2=( ) (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )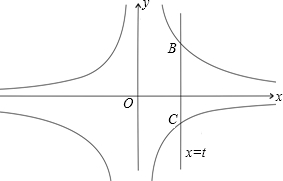 (2012•株洲)如图,直线x=t(t>0)与反比例函数
(2012•株洲)如图,直线x=t(t>0)与反比例函数