题目内容
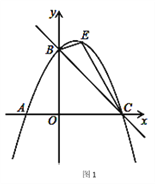
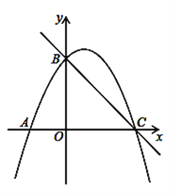
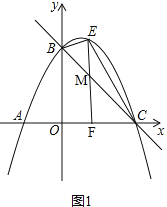
【题目】如图,直线y=﹣x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.
x+c经过B、C两点,点E是直线BC上方抛物线上的一动点.
(1)求抛物线的解析式;
(2)过点E作y轴的平行线交直线BC于点M、交x轴于点F,当S△BEC=![]() 时,请求出点E和点M的坐标;
时,请求出点E和点M的坐标;
(3)在(2)的条件下,当E点的横坐标为1时,在EM上是否存在点N,使得△CMN和△CBE相似?如果存在,请直接写出点N的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)点E的坐标是(1,3)或(2,2),M的坐标是(1,2)或(2,1);
x+3;(2)点E的坐标是(1,3)或(2,2),M的坐标是(1,2)或(2,1);
(3)存在,N(1, ![]() )或N′(1,-10).
)或N′(1,-10).
【解析】试题分析:(1)由直线y=﹣x+3与x轴交于点C,与y轴交于点B,求出点C、B的坐标,代入y=ax2+![]() x+c即可得得解;
x+c即可得得解;
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,设点E的坐标是(x,﹣ ![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣x+3),求出EM的长,利用面积即可得解;
x+3),则点M的坐标是(x,﹣x+3),求出EM的长,利用面积即可得解;
(3)存在.分别求出CB,CM的值,进行分类讨论即可得解.
试题解析:(1)∵直线y=﹣x+3与x轴交于点C,与y轴交于点B,
∴点B的坐标是(0,3),点C的坐标是(3,0)
∵y=ax2+![]() x+c经过B、C两点,
x+c经过B、C两点,
∴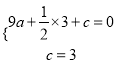
解得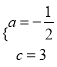
∴y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,
∵点E是直线BC上方抛物线上的一动点,
∴设点E的坐标是(x,﹣ ![]() x2+
x2+![]() x+3),
x+3),
则点M的坐标是(x,﹣x+3),
∴EM=﹣![]() x2+
x2+![]() x+3﹣(﹣x+3)=﹣
x+3﹣(﹣x+3)=﹣![]() x2+
x2+![]() x,
x,
∴S△BEC=S△BEM+S△MEC= ![]()
=![]() ×(﹣
×(﹣![]() x2+
x2+![]() x)×3=﹣
x)×3=﹣![]() x2+
x2+![]() x=
x=![]()
∴﹣![]() x2+
x2+![]() x=
x=![]() ,解之得,x1=1,x2=2
,解之得,x1=1,x2=2
即点E的坐标是(1,3)或(2,2)
此时对应的M的坐标是(1,2)或(2,1).
(3)存在.
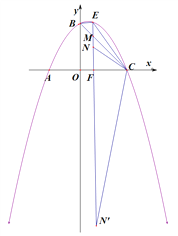
易得∠CBE=∠CEF=45 ,CB=![]() ,CM=
,CM=![]() ,BE=1,
,BE=1,
①当![]() 时,△CMN∽△CBE,
时,△CMN∽△CBE,
即![]() ,得MN=
,得MN=![]() ,
,
∴FN=![]() ,N(1,
,N(1, ![]() )
)
②当![]() 时,△CMN∽△EBC,
时,△CMN∽△EBC,
即![]() ,得MN=12,
,得MN=12,
∴FN=-10,N′(1,-10),
∴在EM上是否存在条件的点N,是N(1, ![]() )或N′(1,-10).
)或N′(1,-10).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案