题目内容
【题目】如图,已知A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(5,2).
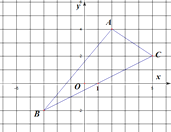
(1)在图中画出△ABC关于y轴对称的△A′B′C′,并写出点A′,B′,C′的坐标;
(2)求△ABC的面积;
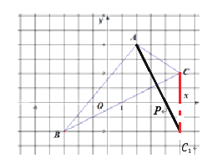
(3)在x轴上找点P,使PA+PC的值最小,并观察图形,写出P点的坐标.
【答案】(1)A′(-2,4), B′(3,-2) ,C′(-5,2);(2) 14;(3)图略,P(4,0)
【解析】试题分析:(1)先根据轴对称性找出△ABC各顶点关于y轴对称的点A′,B′,C′,然后再顺次连接A′,B′,C′,即可得到△A′B′C′,根据坐标系点的位置写出坐标,
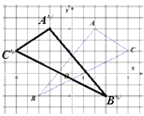
(2)利用三角形所在的矩形的面积减去三角形周围三个直角三角形的面积,然后列式计算,
(3)先作点C关于x轴对称的点![]() ,然后连接
,然后连接![]() ,则
,则![]() 与x轴的交点即所求点P,然后写出此时P点坐标.
与x轴的交点即所求点P,然后写出此时P点坐标.
试题解析:(1)A′(-2,4), B′(3,-2),C′(-5,2),
(2)![]() ,
,
(3)图略P(4,0).

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目