题目内容
【题目】抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线![]() 上,与y轴相交于点D(0,3)。
上,与y轴相交于点D(0,3)。
(1)求抛物线F的解析式;
(2)连结CD、BD,则线段BD与CD的数量关系和位置关系分别为 ;
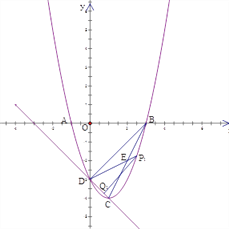
(3)点P为直线CD上方抛物线F上的一个动点,PQ⊥CD,垂足为Q,若∠QPD=∠DBC,求点P的坐标。
【答案】(1)抛物线F的解析式为![]() ;
;
(2)BD⊥CD,BD=3CD;
(3)点P的坐标为P1![]() 和P2(4,5)
和P2(4,5)
【解析】分析:(1)由题意得顶点C(1,-4),设抛物线解析式为;y=a(x-1) -4,把D(0,3)代入即可求解;(2)由D、B、C的坐标,求出线段BD,BC,BC的值,利用定理的逆定理判断;(3)分两种情况讨论①当点Q在点D在下方时;②当点Q在点D在上方时.
本题解析:(1)将x=1代入y=x-5,∴y=-4,∴顶点C(1,-4)
设![]() ,∵过点D(0,-3), ∴a-4=-3,∴a=1,∴
,∵过点D(0,-3), ∴a-4=-3,∴a=1,∴![]() .
.
(2)BD⊥CD,BD=3CD
(3)①当点Q在点D在下方时
∵P1Q1⊥CD, ∴∠P1Q1D=∠BDC=90°
又∵∠DBC=∠Q1P1D
∴∠BCD=∠P1DQ1 ,∴∠BDE=∠DBE
∴ED=EC=BE即E为BC的中点
∴E(2,-2), ∴![]()
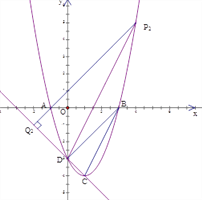
②当点Q在点D在上方时
∵∠P2Q2D=∠BDC=90°∠DBC=∠Q2P2D
∴∠DCB=∠Q2DP2,∴P2D∥BC, ∵B(3,0),C(1,-4),∴![]() ,∵D(0,-3)
,∵D(0,-3)
∴![]() ,∴P2(4,5) ,∴点P的坐标为
,∴P2(4,5) ,∴点P的坐标为![]() 和P2(4,5).
和P2(4,5).

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目