题目内容
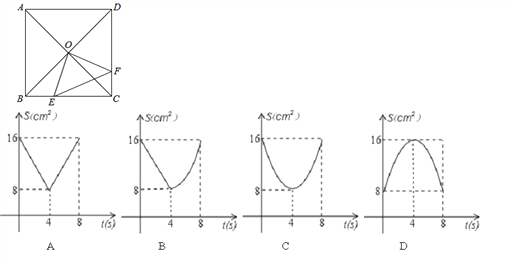
【题目】如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥AB,垂足分别为E、F,请问OF与CD有怎样的数量关系?

【答案】OF=![]() CD.理由见解析.
CD.理由见解析.
【解析】试题分析:连接AO并延长,与⊙O相交于点G,连接BG,根据同弧所对的圆周角相等可得∠G=∠ADB,再根据等角的余角相等求出∠DAE=∠BAG,然后根据相等的圆周角所对的弦相等可得CD=BG,根据垂径定理可得AF=BF,从而得到OF是△ABG的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得OF=![]() BG.
BG.
试题解析:OF=![]() CD.
CD.
理由如下:如图,连接AO并延长,与⊙O相交于点G,连接BG,
则∠G=∠ADB,
∵AC⊥BD,
∴∠DAE+∠ADB=90°,
∵AG是直径,
∴∠BAG+∠G=90°,
∴∠DAE=∠BAG,
∴CD=BG,
∵OF⊥AB,
∴AF=BF,
∴OF是△ABG的中位线,
∴OF=![]() BG,
BG,
故OF=![]() CD.
CD.


练习册系列答案
相关题目