题目内容
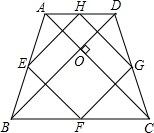 (2012•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.
(2012•南京)如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)求证:四边形EFGH是正方形;
(2)若AD=2,BC=4,求四边形EFGH的面积.
分析:(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.
(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出EH2=
,也即得出了正方形EHGF的面积.
(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出EH2=
| 9 |
| 2 |
解答:证明:(1)在△ABC中,E、F分别是AB、BC的中点,
故可得:EF=
AC,同理FG=
BD,GH=
AC,HE=
BD,
在梯形ABCD中,AB=DC,
故AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.

(2)连接EG.
在梯形ABCD中,
∵E、G分别是AB、DC的中点,
∴EG=
(AD+BC)=3.
在Rt△EHG中,
∵EH2+GH2=EG2,EH=GH,
∴EH2=
,即四边形EFGH的面积为
.
故可得:EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在梯形ABCD中,AB=DC,
故AC=BD,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,
又∵AC⊥BD,
∴EH⊥HG,
∴四边形EFGH是正方形.

(2)连接EG.
在梯形ABCD中,
∵E、G分别是AB、DC的中点,
∴EG=
| 1 |
| 2 |
在Rt△EHG中,
∵EH2+GH2=EG2,EH=GH,
∴EH2=
| 9 |
| 2 |
| 9 |
| 2 |
点评:此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的内角和定理得出EH=HG=GF=FE,这是本题的突破口.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 (2012•南京)如图,在?ABCD中,AD=10cm,CD=6cm,E为AD上一点,且BE=BC,CE=CD,则DE=
(2012•南京)如图,在?ABCD中,AD=10cm,CD=6cm,E为AD上一点,且BE=BC,CE=CD,则DE=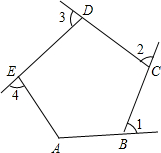 (2012•南京)如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A=120°,则∠1+∠2+∠3+∠4=
(2012•南京)如图,∠1、∠2、∠3、∠4是五边形ABCDE的4个外角.若∠A=120°,则∠1+∠2+∠3+∠4=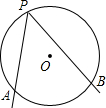 (2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
(2012•南京)如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角. (2012•南京)如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.
(2012•南京)如图,在Rt△ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过点B作BE⊥AC,与BD的垂线DE交于点E.