题目内容
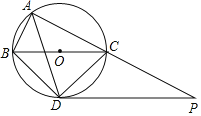
【题目】如图，已知△ABC和△EDC是以点C为位似中心的位似图形，且△ABC和△EDC的周长之比为1：2，点C的坐标为（﹣2，0），若点B的坐标为（﹣5，1），则点D的坐标为（ ）
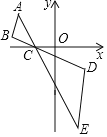
A.（4，﹣2）B.（6，﹣2）C.（8，﹣2）D.（10，﹣2）
【答案】A
【解析】
作BG⊥x轴于点G，DH⊥x轴于点H，根据位似图形的概念得到△ABC∽△EDC，根据相似是三角形的性质计算即可．
作BG⊥x轴于点G，DH⊥x轴于点H，
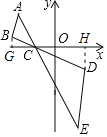
则BG∥DH，
∵△ABC和△EDC是以点C为位似中心的位似图形，
∴△ABC∽△EDC，
∵△ABC和△EDC的周长之比为1：2，
∴
＝
，
由题意得，CG＝3，BG＝1，
∵BG∥DH，
∴△BCG∽△DCH，
∴
＝
＝＝，即
＝
＝，
解得，CH＝6，DH＝2，
∴OH＝CH﹣OC＝4，
则点D的坐标为为（4，﹣2），
故选：A．
暑假作业暑假快乐练西安出版社系列答案
【题目】如图，E为半圆O直径AB上一动点，AB＝6，C为半圆上一定点，连接AC和BC，AD平分∠CAB交BC于点D，连接CE和DE．小红根据学习函数经验，分别对线段AE，CE，DE的长度之间的关系进行了探究．下面是小红的探究过程，请将它补充完整：
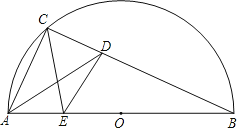
（1）对于点E在直径AB上的不同位置，画图，测量，得到了线段AE，CE，DE的长度的几组值，如下表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
CE/cm | 2.50 | 2.28 | 2.50 | 3.00 | 3.72 | 4.64 | 5.44 |
DE/cm | 2.98 | 2.29 | 1.69 | 1.69 | 2.18 | 3.05 | 3.84 |
AE/cm | 0.00 | 0.87 | 2.11 | 3.02 | 4.00 | 5.12 | 6.00 |
在AECE，DE的长度这三个量中，确定 长度是自变量，自变量的取值范围是 ；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定函数的图象；
（3）结合函数的图象，解决问题：当△ACE为等腰三角形时，AE的长度约为 cm（结果精确到0.01）．
