Question

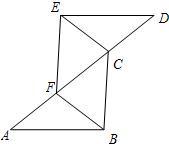17、如图，已知A、F、C、D四点在同一条直线上，AF=CD，∠A=∠D，且AB=DE，则BC=EF，请将下面的说理过程和理由补充完整．
解：∵AF=CD（

已知

）∴AF+FC=CD+（

FC

），
即AC=DF在△ABC和△DEF中
AC=（

DF

）（已证）
∠A=∠D（已知）
AB=（

DE

）（已知）
∴△ABC≌△DEF（

SAS

）
∴BC=EF（

全等三角形对应边相等

）

Answer 1

分析：本题考查的是全等三角形的判定（SAS），填空题有一定的提示作用，相对要简单的多．

解答：解：
∵AF=CD（已知）
∴AF+FC=CD+FC，即AC=DF
在△ABC和△DE
AC=DF（已证）
∠A=∠D（已知）
AB=DE（已知）
∴△ABC≌△DEF（SAS）
∴BC=EF（全等三角形对应边相等）

点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．