题目内容
【题目】【问题探究】
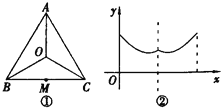
(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
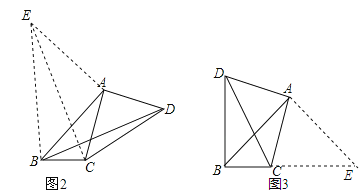
(2)如图2,四边形ABCD中,AB=7cm,BC=3cm,∠ABC=∠ACD=∠ADC=45,求BD的长.
(3)如图3,在(2)的条件下,当△ACD在线段AC的左侧时,求BD的长.

【答案】(1)BD=CE.理由参见解析;(2)![]() cm;(3)(
cm;(3)(![]() )cm.
)cm.
【解析】试题分析:(1)首先根据等式的性质证明∠EAC=∠BAD,则根据SAS即可证明△EAC≌△BAD,根据全等三角形的性质即可证明;
(2)在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC,证明△EAC≌△BAD,证明BD=CE,然后在直角三角形BCE中利用勾股定理即可求解;
(3)在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,证明△EAC≌△BAD,证明BD=CE,即可求解.
试题解析:解:(1)BD=CE.
理由是:∵∠BAE=∠CAD,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE;
(2)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC.∵∠ACD=∠ADC=45°,∴AC=AD,∠CAD=90°,∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE.∵AE=AB=3,∴BE=![]() =
=![]() (不化简不必扣分),∠AEC=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC=
(不化简不必扣分),∠AEC=∠AEB=45°,又∵∠ABC=45°,∴∠ABC+∠ABE=45°+45°=90°,∴EC=![]() =
=![]() =
=![]() ,∴BD=CE=
,∴BD=CE=![]() ;
;
(3)如图3,在线段AC的右侧过点A作AE⊥AB于点A,交BC的延长线于点E,连接BE.∵AE⊥AB,∴∠BAE=90°,又∵∠ABC=45°,∴∠E=∠ABC=45°,∴AE=AB=3,BE=![]() =
=![]() ,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE,∵BC=1,∴BD=CE=
,又∵∠ACD=∠ADC=45°,∴∠BAE=∠DAC=90°,∴∠BAE﹣∠BAC=∠DAC﹣∠BAC,即∠EAC=∠BAD,在△EAC和△BAD中,∵AE=AB,∠EAC=∠BAD,AC=AD,∴△EAC≌△BAD,∴BD=CE,∵BC=1,∴BD=CE=![]() =
=![]() (cm).
(cm).

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案