Question

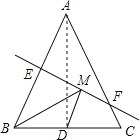
【题目】如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的动点，M为线段EF上一动点，则BM+DM最小值为_____．

Answer 1

【答案】6cm

【解析】

连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．

解：连接AD，

∵△ABC是等腰三角形，点D是BC边的中点，

∴AD⊥BC，

∴S△ABC＝BCAD＝×4×AD＝12，解得AD＝6cm，

∵EF是线段AB的垂直平分线，

∴点B关于直线EF的对称点为点A，

∴AD的长为BM+MD的最小值，

∴BM+DM最小值为6cm，

故答案为：6cm．