题目内容
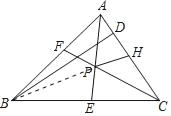
【题目】如图,△ABC角平分线AE、CF交于点P,BD是△ABC的高,点H在AC上,AF=AH,下列结论:①∠APC=90°+![]() ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
ABC;②PH平分∠APC;③若BC>AB,连接BP,则∠DBP=∠BAC﹣∠BCA;④若PH∥BD,则△ABC为等腰三角形,其中正确的结论有_____(填序号).
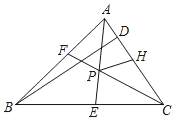
【答案】①④.
【解析】
①利用三角形的内角和定理以及角平分线的定义即可判断.
②利用反证法进行判断.
③根据∠DBP=∠DBC﹣∠PBC=90°﹣∠ACB﹣![]() (180°﹣∠BAC﹣∠ACB)=
(180°﹣∠BAC﹣∠ACB)=![]() (∠BAC﹣∠ACB),由此即可判断.
(∠BAC﹣∠ACB),由此即可判断.
④利用全等三角形的性质证明CA=CB即可判断.
解:∵△ABC角平分线AE、CF交于点P,
∴∠CAP=![]() ∠BAC,∠ACP=
∠BAC,∠ACP=![]() ∠ACB,
∠ACB,
∴∠APC=180°﹣(∠CAP+∠ACP)=180°﹣![]() (∠BAC+∠ACB)=180°﹣
(∠BAC+∠ACB)=180°﹣![]() (180°﹣∠ABC)=90°+
(180°﹣∠ABC)=90°+![]() ∠ABC,故①正确,
∠ABC,故①正确,
∵PA=PA,∠PAF=∠PAH,AF=AH,
∴△PAF≌△PAH(SAS),
∴∠APF=∠APH,
若PH是∠APC的平分线,则∠APF=60°,显然不可能,故②错误,
∵∠DBP=∠DBC﹣∠PBC=90°﹣∠ACB﹣![]() (180°﹣∠BAC﹣∠ACB)=
(180°﹣∠BAC﹣∠ACB)=![]() (∠BAC﹣∠ACB),故③错误,
(∠BAC﹣∠ACB),故③错误,
∵BD⊥AC,PH∥BD,
∴PH⊥AC,
∴∠PHA=∠PFA=90°,
∵∠ACF=∠BCF,CF=CF,∠CFA=∠CFB=90°,
∴△CFA≌△CFB(ASA),
∴CA=CB,故④正确,
故答案为①④.

【题目】某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A | B | |
进价(元/件) | 1200 | 1000 |
售价(元/件) | 1380 | 1200 |
(注:获利=售价-进价)
(1) 该商场购进A、B两种商品各多少件?
(2) 商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?