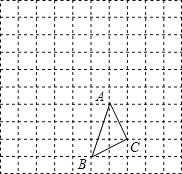
题目内容
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,若分得的两个小三角形中一个三角形为等腰三角形,另一个三角形的三个内角与原来三角形的三个内角分别相等,则称这条线段叫做这个三角形的“等角分割线”.
例如,等腰直角三角形斜边上的高就是这个等腰直角三角形的一条“等角分割线”.

(1)如图1,在△ABC中,D是边BC上一点,若∠B=30°,∠BAD=∠C=40°,求证: AD为△ABC的“等角分割线”;
(2)如图2,△ABC中,∠C=90°,∠B=30°;
①画出△ABC的“等角分割线”,写出画法并说明理由;
②若BC=3,求出①中画出的“等角分割线”的长度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割线”CD,直接写出所有符合要求的∠B的度数.
【答案】(1)见解析(2)①见解析②2(3)44°, 52°, 54°, 108°
【解析】
⑴根据题目中的已知角的度数可以得到∠BAD=∠C=40°,∠ADB=∠BAC=110°
又∠B=∠B,得出△ABD的三个内角与△ABC的三个内角的度数分别相等;根据三角形的外角求出∠ADC=70°,∠BAD+∠CAD=110°得到∠CAD=70°得出△ADC是等腰三角形,所以AD为△ABC的“等角分割线”.
⑵①依据“等角分割线”定义画出即可,②AD平分∠BAC, ∠ACD=30°,设CD=x,则AD=BD=2x,BC=BD+CD=2x+x=3,即可求出AD=2x=2
⑶分△ACD是等腰三角形DA=DC,DA=AC和△BCD是等腰三角形DB=BC,DC=BD四种情况,根据内角和定理及三角形外角等于与它不相邻的两个内角的和计算即可.
(1)证明:∵∠B=30°,∠BAD=∠C=40°
∴∠ADB=∠BAC=110°
又∠B=∠B,
∴△ABD的三个内角与△ABC的三个内角的度数分别相等,
∵∠B=30°,∠BAD=40°,
∴∠ADC=∠B+∠BAD=70°
又∵∠C=40°
∴∠DAC=70°=∠ADC
∴AC=CD
∴△ADC是等腰三角形,
∴AD为△ABC的“等角分割线”
(2)①画法:如图2,画∠BAC的角平分线,交BC于点D,线段AD即为所求,

理由如下:
∵∠C=90°,∠B=30°
∴∠BAC=60°
∵AD平分∠BAC
∴∠DAC =∠BAD =30°=∠B
∴∠ADC=60°=∠BAC
又∵∠C=∠C=90°
∴△ADC的三个内角与△ABC的三个内角的度数分别相等,
∵∠BAD=∠B
∴AD=BD
∴△ABD是等腰三角形,
∴AD为△ABC△ABC的“等角分割线”
②设CD=x
∵△ADC中,∠C=90°,∠DAC=30°,
∴AD=2x,
∴BD=AD=2x
∵BC=3
∴x+2x=3
∴x=1
∴AD=2x=2;
(3) ①当△BCD为等腰三角形,DB=BC时,如下图

∵DB=BC,△ABC∽△ACD
∴ ∠2=∠3,∠1=∠B
∵∠2=∠A+∠1,∠2+∠3+∠B=180°
∴ 2(∠A+∠1)+∠B=180°
∴ 2(24°+∠B)+∠B=180°
∴ ∠B=44°
②当△BCD是等腰三角形,DB=DC时,如下图
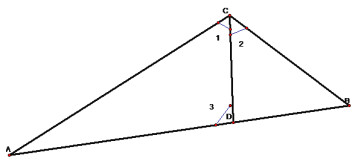
∵DB=DC,△ABC∽△ACD
∴∠B=∠2,∠1=∠B
∵ ∠3=∠2+∠B,∠A+∠1+∠3=180°
∴ ∠A+∠1+∠3=24°+∠B+∠B+∠B=180°
∴ ∠B=52°
③当△ACD为等腰三角形,DA=CA时,如下图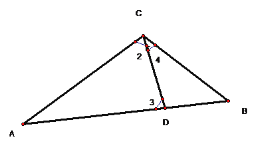
∠2+∠3=180°-∠A=180°-24°=156°
∠2=∠3=78°
∵△ABC∽△CBD
∴∠A=∠4=24°
∵ ∠B+∠4=∠3
∴∠B=54°
当△ACD为等腰三角形,DA=DC时,如下图

∵ DA=DC
∴ ∠A=∠1=24°
∴ ∠2=∠A+∠1=48°
∵△ABC∽△CBD
∴ ∠B=∠2+∠3=∠2+∠A=108°
44°, 52°, 54°, 108°.