题目内容
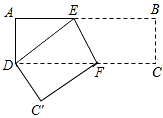如图：长方形纸片ABCD中，AD=4cm，AB=10cm，按如图的方式折叠，使点B与点D重合．折痕为EF，则DE长为
- A.4.8
- B.5
- C.5.8
- D.6
C
分析：注意发现：在折叠的过程中，BE=DE，从而设BE即可表示AE，在直角三角形ADE中，根据勾股定理列方程即可求解．
解答：设DE=xcm，则BE=DE=x，AE=AB-BE=10-x，
在RT△ADE中，DE2=AE2+AD2，即x2=（10-x）2+16．
解得：x=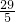
=5.8（cm）．
故选C．
点评：此题考查了翻折变换的知识，解答本题的关键是掌握翻折前后对应线段相等，另外要熟练运用勾股定理解直角三角形．
分析：注意发现：在折叠的过程中，BE=DE，从而设BE即可表示AE，在直角三角形ADE中，根据勾股定理列方程即可求解．
解答：设DE=xcm，则BE=DE=x，AE=AB-BE=10-x，
在RT△ADE中，DE2=AE2+AD2，即x2=（10-x）2+16．
解得：x=
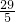=5.8（cm）．故选C．
点评：此题考查了翻折变换的知识，解答本题的关键是掌握翻折前后对应线段相等，另外要熟练运用勾股定理解直角三角形．
练习册系列答案
相关题目
如图，长方形纸片ABCD中，AD=9，AB=3，将其折叠，使其点D与点B重合，点C至点C′，折痕为EF．求△BEF的面积？
23、如图，长方形纸片ABCD，沿折痕AE折叠边AD，使点D落在BC边上的点F处，已知AB=8，S△ABF=24，求EC的长．
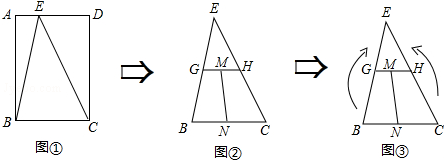
如图，长方形纸片ABCD中，AD=BC=7，沿对称轴EF折叠，若折叠后A′B′与C′D′间的距离为6，则原纸片的宽AB=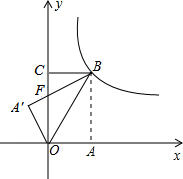
如图，长方形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y）轴上，连结OB，将纸片OABC沿OB折叠，使点A落在点A′处，A′B与y轴交于点F，且知OA=1，AB=2．